路径规划与轨迹跟踪 2 —— 全局路径规划_蚁群算法
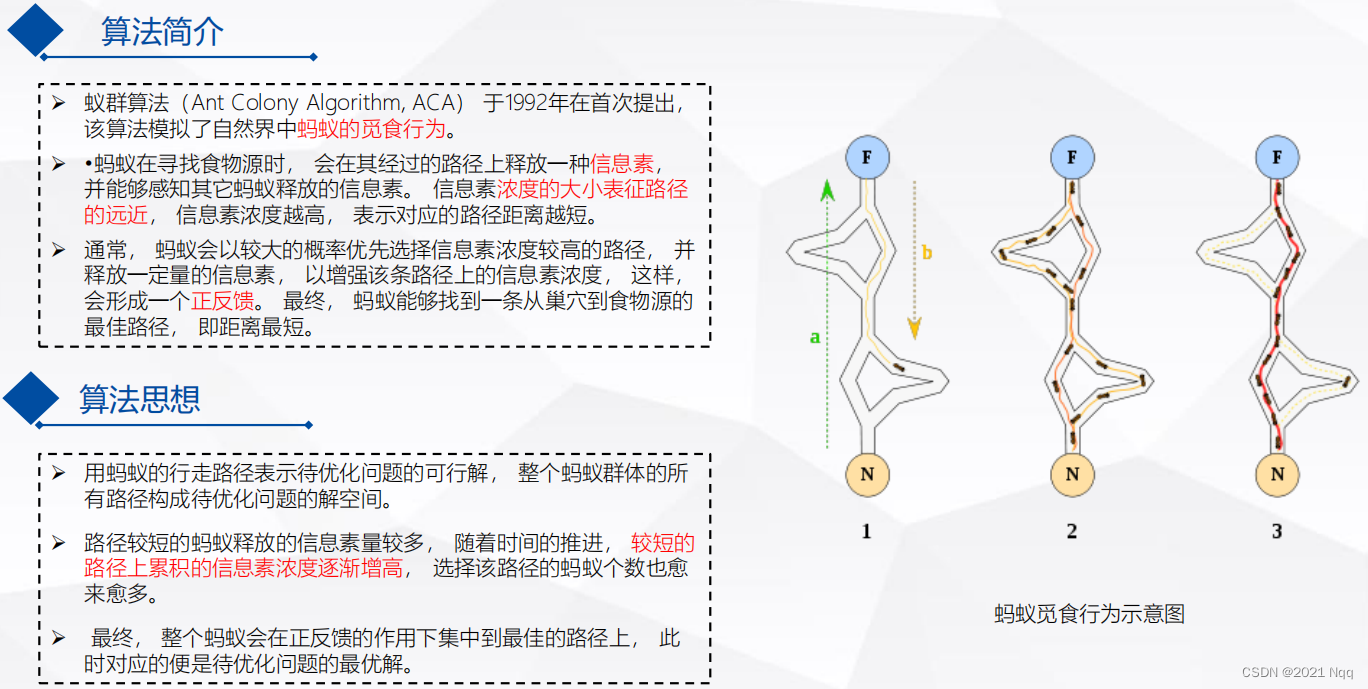
蚁群算法
·
算法思想
- 蚂蚁走的路径越长,则单位距离的信息浓度就会低,所以距离越短的路径,释放的信息素越浓
- 计算下一个节点的访问概率

元胞数组后面()的解释
MATLAB元胞数组()与{}的区别 - {}与()的区别:()是获取的元胞数据,{}直接获取元胞里包含的数据
% 计算下一个节点的访问概率
P = neighbor;
for k = 1:length(P)
P(2,k) = nodes_data{node_step, 4}(k)^alpha * nodes_data{node_step, 5}(k)^beta;
end
P(2,:) = P(2,:)/sum(P(2,:)); % 邻近节点的概率
- 信息素浓度更新
- 蚂蚁自身携带的信息素浓度是固定的,走的路径越长,则单位路径信息素浓度越低,Q表示每只蚂蚁身上携带的相同信息素。每一段路都携带相同的信息素。
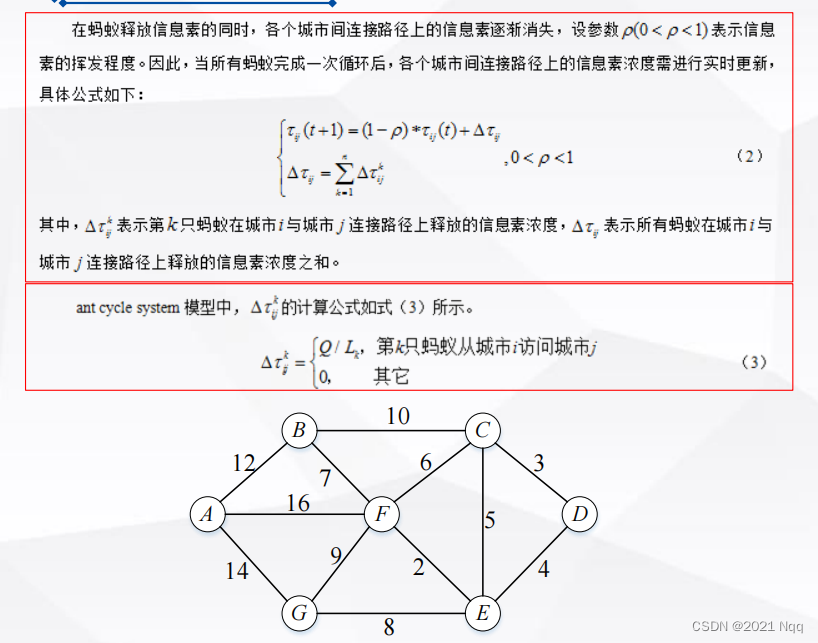
- 备注:启发函数eta的值和城市i与j之间信息素浓度值的计算方式是相同的
- nodes_data{i,3}表示的是不同节点之间的距离值
nodes_data{i,5} = 1./nodes_data{i,3};% x是矩阵时,1./x表示矩阵中每一个元素的倒数
- 流程图
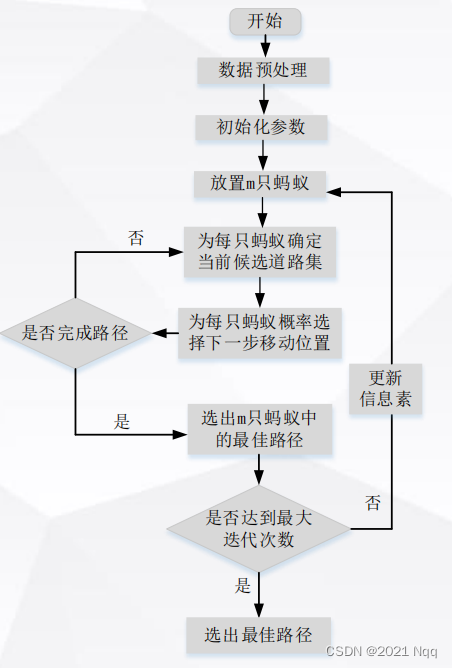
算法精讲
cumsum 和 sum 的区别
(a,b) = min(A) 的含义
% ACA算法
clc
clear
close all
%% 初始化参数
% 根据节点的邻近节点表及字母节点-数字节点对应表,构造节点元胞数组
nodes_data = cell(0);
nodes_data(1,:) = {1, [2, 6, 7], [12, 16, 14]};% 节点1与节点2,6,7相连接,且之间距离为12,16,14
nodes_data(2,:) = {2, [1, 3, 6], [12, 10, 7]};
nodes_data(3,:) = {3, [2, 4, 5, 6], [10, 3, 5, 6]};
nodes_data(4,:) = {4, [3, 5], [3, 4]};
nodes_data(5,:) = {5, [3, 4, 6, 7], [5, 4, 2, 8]};
nodes_data(6,:) = {6, [1, 2, 3, 5, 7], [16, 7, 6, 2, 9]};
nodes_data(7,:) = {7, [1, 5, 6], [14, 8, 9]};
% 始末节点
node_start = 4; % 初始源节点
node_end = 1; % 终节点
% 蚁群相关定义
m = 50; % 蚂蚁数量
n = size(nodes_data,1); % 节点数量(7)。size(X,dim)得到数组X的某维度长度,dim = 1为行数,dim = 2为列数
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常数,表示蚂蚁每次携带的信息素为1
% 迭代过程中,相关参数初始化定义
iter = 1; % 迭代次数初值
iter_max = 100; % 最大迭代次数, 100
Route_best = cell(iter_max,1); % 各代最佳路径, 每一代蚂蚁都是50只,可以生成一条路径。生成100行1列的元胞数组
Length_best = zeros(iter_max,1); % 各代最佳路径的长度, 生成100行1列的0矩阵
Length_ave = zeros(iter_max,1); % 各代路径的平均长度, 生成100行1列的0矩阵
% 将信息素、信息素挥发浓度因子(理解为i与j之间连接路径的信息素浓度)一并放入nodes_data中
Delta_Tau_initial = nodes_data(:,1:2);% 把nodes_data第1、2列元胞数组赋值给Delta_Tau_initial
for i = 1:size(nodes_data,1) % size(nodes_data,1) = 7,size(X,dim)得到数组X的某维度长度,dim = 1,为行数
% 第 4 列信息素个数 = 第 3 列邻接节点长度的个数,每个初始为 1*3(或1*4,根据有几个相关连接点确定的) 的1矩阵
nodes_data{i,4} = ones(1, length(nodes_data{i,3})); % 信息素to(t)初始化为1,下标为ij,后面会进行信息素更新
% node_data{i,5}是对应启发函数值eta
% 第 5 列信息素浓度因子个数 = 第 3 列邻接节点长度的个数
nodes_data{i,5} = 1./nodes_data{i,3}; % x是矩阵时,1./x表示矩阵中每一个元素的倒数
Delta_Tau_initial{i,3} = zeros(1, length(nodes_data{i,3}));% 生成1行length列的0矩阵
end
%% 迭代寻找最佳路径
while iter <= iter_max
route = cell(0); % 初始化路径route为元胞数组,每个蚂蚁访问的节点数量并不一样,需要用元胞存储
% 逐个蚂蚁路径选择
for i = 1:m % m = 50
% 逐个节点路径选择
neighbor = cell(0); % 初始化邻近节点(当前点的邻近节点)
node_step = node_start; % 将起点赋值给第1个蚂蚁,node_start = 4
path = node_step; % 路径初始化,path是一个数组,这里是将起始点添加到数组path
dist = 0; % 距离初始化
% L= ismember(A,B),~ismenmber表示不在
% 如果A中某位置的数据能在B中找到,将返回一个在该位置包含逻辑值 1 (true) 的数组L,数组L其他位置将包含逻辑值 0 (false)
% 当路径表里面包含了终节点时,该蚂蚁完成路径寻优,跳出循环
% 如果node_end(终点)能在path中找到,则ismember(node_end, path)返回true,则循环结束跳出
while ~ismember(node_end, path) % 表示终点不在路径中,就进行循环
% 寻找邻近节点
% 当前节点的邻近节点赋值给neighbour,里面存的是当前点的各个邻近节点
% node_step表示当前路径点,{node_step,2}求的是当前点有哪些邻近节点
neighbor = nodes_data{node_step,2};
% 删除已经访问过的邻近节点
idx = []; % idx是一维数组
for k = 1:length(neighbor) % k = 1:3或者1:4,根据邻近节点的个数确定
if ismember(neighbor(k), path) % 判断 neighbor 里面的节点是否在路径点 path 数组里面
idx(end + 1) = k; % 如果在的话,idx 收集已访问节点的索引。end + n:增加n行或列
end
end
neighbor(idx) = []; % 根据neighbor已访问节点的索引进行清零。前面可知neighbor数组
% 判断是否进入死胡同,若是,直接返回到起点,重新寻路
if isempty(neighbor) % 判断neighbor是否为空,为空则返回1,重新开始
neighbor = cell(0);
node_step = node_start;
path = node_step;
dist = 0;
continue
end
% 计算下一个节点的访问概率
P = neighbor; % 这里 P 和 neighbour 均存储当前点的所有未在path数组的邻近节点
for k = 1:length(P) % ()是以元胞数组进行访问的,k表示第k个邻近节点
P(2,k) = nodes_data{node_step, 4}(k)^alpha * nodes_data{node_step, 5}(k)^beta;
end
P(2,:) = P(2,:)/sum(P(2,:)); % 各个邻近节点的访问概率,为后面轮盘赌法选择下一个访问节点做准备
% 每个点求出的概率值再除以总的值,保证各个邻近节点的概率和为1
% 最后结果P的值是2*1的列向量,第一个1表示终点,第二个1表示概率和
% cumsum 计算一个数组各行的累加值,累积和
% A=[1;2;3;4;5] 则 cumsum(A) = [1;3;6;10;15](默认是列方向求累积和)计算之后,A大小维度不变
% 轮盘赌法:比如各个节点概率为 0.2 0.3 0.5,加起来等于1,可以分为0-0.2,0.2-0.5,0.5-1.0三个区间
% 轮盘赌法选择下一个访问节点
Pc = cumsum(P(2,:)); % 列方向的累积和(对应轮盘赌的累加区间)
Pc = [0, Pc]; % 添加0,这样形成从0开始的区间,[0,..]
% rand 返回一个在区间 (0,1) 内均匀分布的随机数,rand(n) 返回一个 n×n 的随机数矩阵
randnum = rand; % 生成一个(0,1)之间的随机数
for k = 1:length(Pc)-1 % -1是因为上面一行Pc数组开头多添加一个0
if randnum > Pc(k) && randnum < Pc(k+1) % 下标从1开始
target_node = neighbor(k);% 选择下标为k的点作为下一个目标点
end
end
% 计算单步距离
% find函数,返回符合条件的索引值
idx_temp = find(nodes_data{node_step, 2} == target_node);% 如果在当前节点的邻近节点集合中发现目标节点
dist = dist + nodes_data{node_step, 3}(idx_temp); % 添加距离长度到dist
% 更新下一步的目标节点及路径集合
node_step = target_node;
path(end + 1) = node_step;
end
% 上面是第i只蚂蚁循环结束
% 存放第i只蚂蚁的累计距离及对应路径
Length(i,1) = dist; % Length是50*1的列向量,route是元胞数组
route{i,1} = path; % path存的是第i只蚂蚁的路径,route存的是一代50只蚂蚁路径
end % 到这里完成了m只蚂蚁的遍历
%% 计算这一代的m只蚂蚁中最短距离及对应路径
if iter == 1
% [a,b] = min(c)返回的a为c中每一列最小的元素组成的集合,b为每一列中最小元素所在的行数组成的集合
% [C,I] = min(A)找到A中那些最⼩值的索引位置,将他们放在向量I中返回,C存放的是最小值
% 如果这⾥有多个相同最⼩值时,返回第⼀个的索引到I中
[min_Length,min_index] = min(Length); % min_Length是Length中最小值,min_index是Length最小值第1个索引位置
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length); % 路径平均值
Route_best{iter,1} = route{min_index,1};
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length); % 比较Length_best里上一代和这一代的最小值
Length_ave(iter) = mean(Length); % 路径平均值
if Length_best(iter) == min_Length % 如果这一代的最小值为最小,则当前一代的路径添加到最佳路径
Route_best{iter,1} = route{min_index,1}; % Route是元胞数组,Length_best、Length、Length_ave都是矩阵(列向量)
else
Route_best{iter,1} = Route_best{iter - 1,1}; % 否则将上一代的最佳路径作为这代最佳路径
end
end
%% 更新信息素
% 计算每一条路径上的经过的蚂蚁留下的信息素
Delta_Tau = Delta_Tau_initial;
% 逐个蚂蚁计算
for i = 1:m
% 逐个节点间计算
for j = 1:length(route{i,1})-1 % 因为是节点间,所以数量比节点少1个
node_start_temp = route{i,1}(j);
node_end_temp = route{i,1}(j + 1);
idx = find(Delta_Tau{node_start_temp, 2} == node_end_temp);
Delta_Tau{node_start_temp,3}(idx) = Delta_Tau{node_start_temp,3}(idx) + Q/Length(i);
end
end
% 考虑挥发因子,更新信息素(一代50只蚂蚁走完进行信息素更新)
for i = 1:size(nodes_data, 1)
nodes_data{i, 4} = (1-rho) * nodes_data{i, 4} + Delta_Tau{i, 3};
end
% 更新迭代次数
iter = iter + 1;
end
%% 绘图、结果
figure
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')
% 最优路径
[dist_min, idx] = min(Length_best);
path_opt = Route_best{idx,1};

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容







所有评论(0)