二十六、搜索与图论——SPFA算法(单源最短路 + 负权边 + Bellman-Ford 时间复杂度优化)
SPFA算法
·
SPFA算法主要内容
一、基本思路
1、算法概念
-
概念:
-
- SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称,通常用于求含负权边的单源最短路径,以及判负权环。SPFA一般情况复杂度是O(m), 最坏情况下复杂度和朴素 Bellman-Ford 相同,为O(nm)。
-
原 Bellman-Ford 算法步骤 :
-
- for n次
for 所有边 a,b,w (松弛操作)
dist[b] = min(dist[b],back[a] + w)
- for n次
-
- spfa算法对第二行中所有边进行松弛操作进行了优化,原因是在bellman—ford算法中,即使该点的最短距离尚未更新过,但还是需要用尚未更新过的值去更新其他点,由此可知,该操作是不必要的,我们只需要找到更新过的值去更新其他点即可,此处即为优化点。
2、SPFA 算法步骤
算法步骤
- 1. queue <– 1
- 2. while queue 不为空
-
- (1) t <– 队头 —— 取队头
-
-
- queue.pop() —— 删掉头结点
-
-
- (2) 用 t 更新所有出边 t –> b,权值为w
-
-
- queue <– b (若该点被更新过,则拿该点更新其他点)
-
注意事项
-
- 与堆优化版的Dijkstra算法相比:堆优化版使用的是小根堆的排序之后的头结点进行更新(遍历的是距离最近点),SPFA算法是只要该点距离更新了,那就可以加入队列更新其他点。
-
- Dijkstra 算法一般用SPFA算法也可以,但是若为网格图,则可能会卡为O(mn)
3、SPFA算法进行负环判断
-
求负环的常用方法,基于SPFA,一般都用方法 2:
-
方法 1: 统计每个点入队的次数,如果某个点入队n次,则说明存在负环
-
方法 2: 统计当前每个点的最短路中所包含的边数,如果某点的最短路所包含的边数大于等于n,则也说明存在环。
-
每次做一遍spfa()一定是正确的,但时间复杂度较高,可能会超时。
-
初始时将所有点插入队列中可以按如下方式理解:
-
- 在原图的基础上新建一个虚拟源点,从该点向其他所有点连一条权值为0的有向边。那么原图有负环等价于新图有负环。此时在新图上做spfa,将虚拟源点加入队列中。然后进行spfa的第一次迭代,这时会将所有点的距离更新并将所有点插入队列中。执行到这一步,就等价于视频中的做法了。那么视频中的做法可以找到负环,等价于这次spfa可以找到负环,等价于新图有负环,等价于原图有负环。得证。
-
求负环算法步骤:
-
- dist[x] 记录虚拟源点到x的最短距离
-
- cnt[x] 记录当前x点到虚拟源点最短路的边数,初始每个点到虚拟源点的距离为0,只要他能再走n步,即cnt[x] >= n,则表示该图中一定存在负环,由于从虚拟源点到x至少经过n条边时,则说明图中至少有n + 1个点,表示一定有点是重复使用
-
- 若dist[j] > dist[t] + w[i],则表示从t点走到j点能够让权值变少,因此进行对该点j进行更新,并且对应cnt[j] = cnt[t] + 1,往前走一步
-
注意:
-
该题是判断是否存在负环,并非判断是否存在从1开始的负环,因此需要将所有的点都加入队列中,更新周围的点.

二、Java、C语言模板实现
SPFA 算法
//Java 模板实现
static int N = 100010;
static int idx = 0;
static int INF = 0x3f3f3f3f;
static int[] h = new int[N];
static int[] e = new int[N];
static int[] ne = new int[N];
static int[] w = new int[N];
static int[] dis = new int[N];
static boolean[] st = new boolean[N]; // 判断是否在更新队列中
static int n,m;
static int x,y,c;
static void add(int a, int b, int c){ // 图的存储,其中存在负权边
e[idx] = b;
ne[idx] = h[a];
w[idx] = c;
h[a] = idx++;
}
static String spfa(){
PriorityQueue<Integer> q = new PriorityQueue<Integer>(); // 存储的是所有“更新距离”的点
// 此处的队列和堆优化的Dijkstra算法的区别在于,堆优化的需要通过小根堆,找到距离最近的点进行更新
// 而这里使用的是队列存储“更新距离”的点
dis[1] = 0; // 初始化第一个点的距离为 0
q.add(1); // 将第一个点加入队列
st[1] = true; // 标记点 1 在队列中
while(!q.isEmpty()){
int t = q.poll();
st[t] = false; // 表明这个点已经弹出队列中,也就是“不在更新了距离”的队列
for(int i = h[t]; i != -1; i = ne[i]){ // 遍历“更新点”可以连接到的点,用它来更新其他点
int newNode = e[i]; // 存的是点b,也就是出边对应点
if(dis[newNode] > dis[t] + w[i]){ // 判断是否可以进行距离更新
dis[newNode] = dis[t] + w[i];
// 需要使用这个点进行其他点的更新,因此需要加入队列
// 判断点是否在队列,如果不在队列中,那就将它加入
if(st[newNode] == false){
q.add(newNode);
st[newNode] = true; // 表明这个点在“更新距离”队列
}
}
}
}
if(dis[n] == INF){
return "impossible";
}
return dis[n] + "";
}
```cpp
// C++实现,此处是yxc实现
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储每个点到1号点的最短距离
bool st[N]; // 存储每个点是否在队列中
// 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入
{
q.push(j);
st[j] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
SPFA求负环
static int N = 100010;
static int idx = 0;
static int INF = 0x3f3f3f3f;
static int[] h = new int[N];
static int[] e = new int[N];
static int[] ne = new int[N];
static int[] w = new int[N];
static int[] dis = new int[N];
static int[] count = new int[N]; // 判断到达这个点,需要经过的路径条数
static boolean[] st = new boolean[N]; // 判断是否在更新队列中
static int n,m;
static int x,y,c;
static void add(int a, int b, int c){ // 图的存储,其中存在负权边
e[idx] = b;
ne[idx] = h[a];
w[idx] = c;
h[a] = idx++;
}
static String spfa(){
PriorityQueue<Integer> q = new PriorityQueue<Integer>(); // 存储的是所有“更新距离”的点
// 此处的队列和堆优化的Dijkstra算法的区别在于,堆优化的需要通过小根堆,找到距离最近的点进行更新
// 而这里使用的是队列存储“更新距离”的点
dis[1] = 0; // 初始化第一个点的距离为 0
// 因为有些存在负环,但是并不能实现从1到负环点
// 所以就把所有店加入队列中,这样哪怕从1 没有路径到达,但是依旧可以实现遍历进行环的循环
// 加入到了负环点实际是可以一直转圈圈的死循环,因此可以仅仅使用n来进行判断是否存在负环点
for(int i = 1; i <= n; i++){
q.add(i); // 将点加入队列
st[i] = true; // 标记点在队列中
}
while(!q.isEmpty()){
int t = q.poll();
st[t] = false; // 表明这个点已经弹出队列中,也就是“不在更新了距离”的队列
for(int i = h[t]; i != -1; i = ne[i]){ // 遍历“更新点”可以连接到的点,用它来更新其他点
int newNode = e[i]; // 存的是点b,也就是出边对应点
if(dis[newNode] > dis[t] + w[i]){ // 判断是否可以进行距离更新
dis[newNode] = dis[t] + w[i];
count[newNode] = count[t] + 1;
if(count[newNode] >= n){
return "Yes";
}
// 需要使用这个点进行其他点的更新,因此需要加入队列
// 判断点是否在队列,如果不在队列中,那就将它加入
if(st[newNode] == false){
q.add(newNode);
st[newNode] = true; // 表明这个点在“更新距离”队列
}
}
}
}
return "No";
}
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N], cnt[N]; // dist[x]存储1号点到x的最短距离,cnt[x]存储1到x的最短路中经过的点数
bool st[N]; // 存储每个点是否在队列中
// 如果存在负环,则返回true,否则返回false。
bool spfa()
{
// 不需要初始化dist数组
// 原理:如果某条最短路径上有n个点(除了自己),那么加上自己之后一共有n+1个点,由抽屉原理一定有两个点相同,所以存在环。
queue<int> q;
for (int i = 1; i <= n; i ++ )
{
q.push(i);
st[i] = true;
}
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true; // 如果从1号点到x的最短路中包含至少n个点(不包括自己),则说明存在环
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
三、例题题解
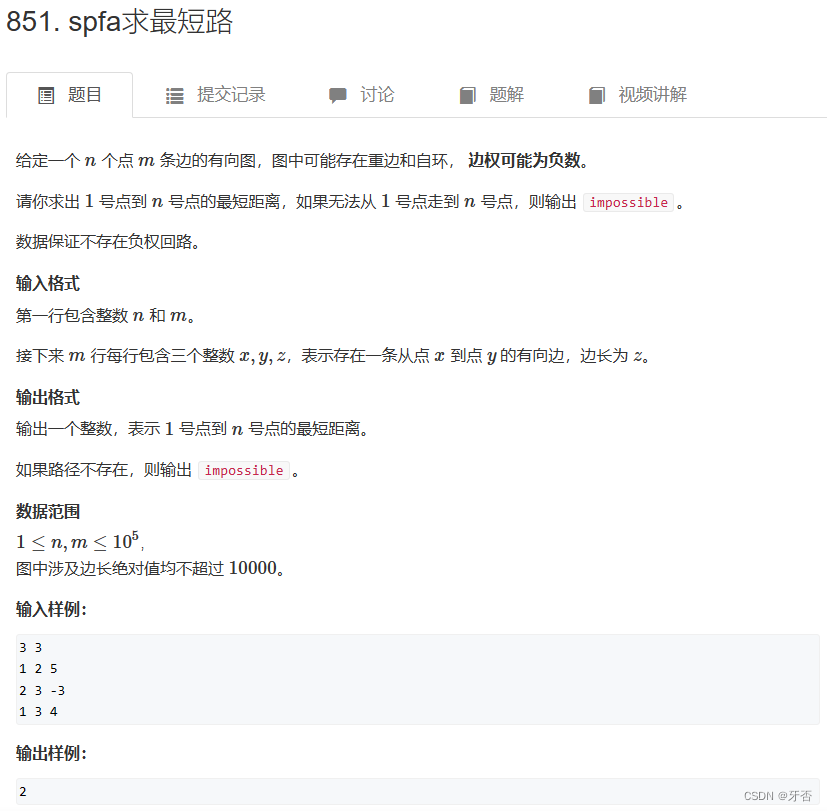
// java题解实现
import java.util.*;
public class Main{
static int N = 100010;
static int idx = 0;
static int INF = 0x3f3f3f3f;
static int[] h = new int[N];
static int[] e = new int[N];
static int[] ne = new int[N];
static int[] w = new int[N];
static int[] dis = new int[N];
static boolean[] st = new boolean[N]; // 判断是否在更新队列中
static int n,m;
static int x,y,c;
static void add(int a, int b, int c){ // 图的存储,其中存在负权边
e[idx] = b;
ne[idx] = h[a];
w[idx] = c;
h[a] = idx++;
}
static String spfa(){
PriorityQueue<Integer> q = new PriorityQueue<Integer>(); // 存储的是所有“更新距离”的点
// 此处的队列和堆优化的Dijkstra算法的区别在于,堆优化的需要通过小根堆,找到距离最近的点进行更新
// 而这里使用的是队列存储“更新距离”的点
dis[1] = 0; // 初始化第一个点的距离为 0
q.add(1); // 将第一个点加入队列
st[1] = true; // 标记点 1 在队列中
while(!q.isEmpty()){
int t = q.poll();
st[t] = false; // 表明这个点已经弹出队列中,也就是“不在更新了距离”的队列
for(int i = h[t]; i != -1; i = ne[i]){ // 遍历“更新点”可以连接到的点,用它来更新其他点
int newNode = e[i]; // 存的是点b,也就是出边对应点
if(dis[newNode] > dis[t] + w[i]){ // 判断是否可以进行距离更新
dis[newNode] = dis[t] + w[i];
// 需要使用这个点进行其他点的更新,因此需要加入队列
// 判断点是否在队列,如果不在队列中,那就将它加入
if(st[newNode] == false){
q.add(newNode);
st[newNode] = true; // 表明这个点在“更新距离”队列
}
}
}
}
if(dis[n] == INF){
return "impossible";
}
return dis[n] + "";
}
public static void main(String[] args){
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
for(int i = 0; i < N; i++){
dis[i] = INF;
h[i] = -1;
}
for(int i = 0; i < m; i++){
x = in.nextInt();
y = in.nextInt();
c = in.nextInt();
add(x, y, c);
}
String result = spfa();
System.out.println(result);
}
}
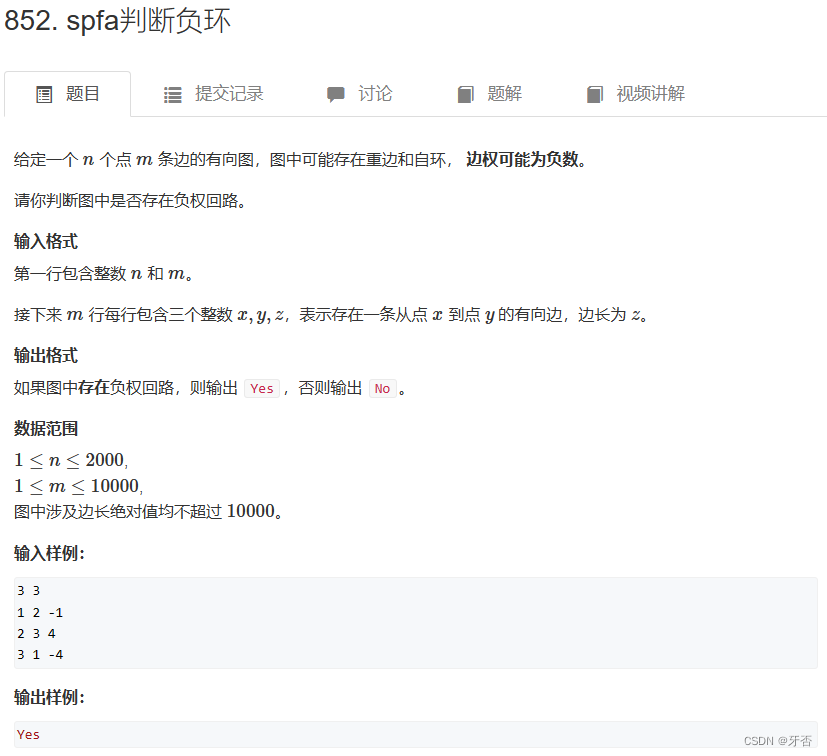
import java.util.*;
public class Main{
static int N = 100010;
static int idx = 0;
static int INF = 0x3f3f3f3f;
static int[] h = new int[N];
static int[] e = new int[N];
static int[] ne = new int[N];
static int[] w = new int[N];
static int[] dis = new int[N];
static int[] count = new int[N]; // 判断到达这个点,需要经过的路径条数
static boolean[] st = new boolean[N]; // 判断是否在更新队列中
static int n,m;
static int x,y,c;
static void add(int a, int b, int c){ // 图的存储,其中存在负权边
e[idx] = b;
ne[idx] = h[a];
w[idx] = c;
h[a] = idx++;
}
static String spfa(){
PriorityQueue<Integer> q = new PriorityQueue<Integer>(); // 存储的是所有“更新距离”的点
// 此处的队列和堆优化的Dijkstra算法的区别在于,堆优化的需要通过小根堆,找到距离最近的点进行更新
// 而这里使用的是队列存储“更新距离”的点
dis[1] = 0; // 初始化第一个点的距离为 0
// 因为有些存在负环,但是并不能实现从1到负环点
// 所以就把所有店加入队列中,这样哪怕从1 没有路径到达,但是依旧可以实现遍历进行环的循环
// 加入到了负环点实际是可以一直转圈圈的死循环,因此可以仅仅使用n来进行判断是否存在负环点
for(int i = 1; i <= n; i++){
q.add(i); // 将点加入队列
st[i] = true; // 标记点在队列中
}
while(!q.isEmpty()){
int t = q.poll();
st[t] = false; // 表明这个点已经弹出队列中,也就是“不在更新了距离”的队列
for(int i = h[t]; i != -1; i = ne[i]){ // 遍历“更新点”可以连接到的点,用它来更新其他点
int newNode = e[i]; // 存的是点b,也就是出边对应点
if(dis[newNode] > dis[t] + w[i]){ // 判断是否可以进行距离更新
dis[newNode] = dis[t] + w[i];
count[newNode] = count[t] + 1;
if(count[newNode] >= n){
return "Yes";
}
// 需要使用这个点进行其他点的更新,因此需要加入队列
// 判断点是否在队列,如果不在队列中,那就将它加入
if(st[newNode] == false){
q.add(newNode);
st[newNode] = true; // 表明这个点在“更新距离”队列
}
}
}
}
return "No";
}
public static void main(String[] args){
Scanner in = new Scanner(System.in);
n = in.nextInt();
m = in.nextInt();
for(int i = 0; i < N; i++){
dis[i] = INF;
h[i] = -1;
}
for(int i = 0; i < m; i++){
x = in.nextInt();
y = in.nextInt();
c = in.nextInt();
add(x, y, c);
}
String result = spfa();
System.out.println(result);
}
}

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容







所有评论(0)