计算机视觉目标检测——DETR代码解读
本周主要对DETR(End-to-End Object Detection with Transformers)的代码实现进行了详细解读和学习。DETR是首个将目标检测任务转化为集合预测问题的端到端框架,通过Transformer的全局建模能力,显著简化了检测器的设计。在代码解读中,重点分析了DETR的整体架构,包括CNN特征提取、正余弦位置编码、Transformer的Encoder-Decod
计算机视觉目标检测——DETR代码解读
文章目录
摘要
本周主要对DETR(End-to-End Object Detection with Transformers)的代码实现进行了详细解读和学习。DETR是首个将目标检测任务转化为集合预测问题的端到端框架,通过Transformer的全局建模能力,显著简化了检测器的设计。在代码解读中,重点分析了DETR的整体架构,包括CNN特征提取、正余弦位置编码、Transformer的Encoder-Decoder结构和基于集合预测的损失函数。Transformer模块通过多头注意力机制构建全局上下文关系,而损失函数利用匈牙利算法实现预测框与真实框的一对一匹配,避免了传统方法中的NMS后处理。代码展示了DETR在架构上的高效性与简洁性。
Abstract
This week’s work focused on a comprehensive analysis of the code implementation for DETR (End-to-End Object Detection with Transformers). DETR represents a pioneering framework that reformulates object detection as a set prediction task, eliminating the need for post-processing steps like NMS. The study explored the overall architecture of DETR, including CNN-based feature extraction, sine positional encoding, the Transformer-based encoder-decoder structure, and the set prediction loss function. The Transformer module leverages multi-head attention mechanisms to establish global contextual relationships, while the loss function employs the Hungarian algorithm to achieve one-to-one matching between predicted and ground-truth boxes. The code demonstrates the efficiency and simplicity of DETR’s design.
一、DETR代码解读
1. 整体代码
1.1 整体架构
先回顾一下DETR的整体框架:
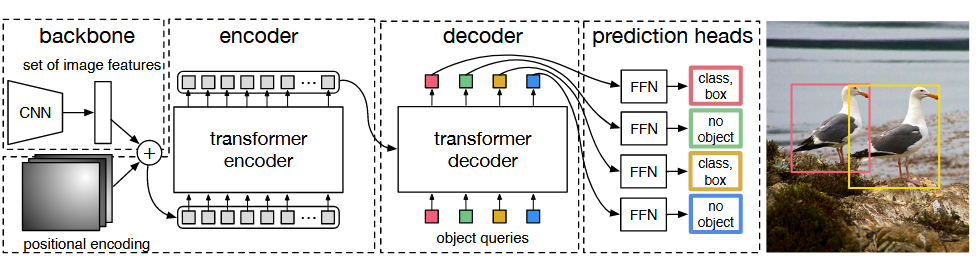
DETR的网络结构主要由三部分组成:CNN骨干网、Transformer编码器和解码器,以及输出层。
- CNN骨干网:负责从输入图像中提取特征图。DETR通常使用ResNet等深度卷积神经网络作为骨干网,通过一系列的卷积和池化操作,将输入图像转换为高维特征图。
- Transformer编码器:用于对CNN骨干网提取的特征图进行编码。编码器由多个Transformer block组成,每个block包含自注意力层和前馈神经网络层。通过多层自注意力机制,编码器能够捕获特征图中不同位置之间的全局上下文关系,生成一组特征向量。
- Transformer解码器:解码器是DETR实现集合预测的关键部分。它接受编码器的输出和一组可学习的目标查询(object queries),通过自注意力机制和编码器-解码器注意力机制,将目标查询解码为一系列目标的边界框坐标和类别标签。
- 预测头:两个简单的前馈网络( feed forward network,FFN )来进行最终的检测预测。分别用于预测边界框的标准化中心坐标、高度和宽度,以及类别标签。
1.2 基于集合预测的损失函数
DETR在单次通过解码器时推断一个固定大小的有 N 个预测的集合,其中 N 被设置为显著大于图像中典型的物体数量,文中N为100。训练的主要困难之一是在 ground truth 方面对预测对象(类别、位置、大小)进行打分。我们的损失在预测对象和真实对象之间产生一个最佳的二分匹配,然后优化 object-specific ( bounding box ) 的损失。
用 y y y表示对象的ground truth集合, y ^ = { y ^ i } i = 1 N \hat y = \{ {\hat y_i}\} _{i = 1}^N y^={y^i}i=1N表示有 N N N个预测的集合。假设N远大于图像中物体的个数,我们考虑y也是一个大小为N的被 ( no object ) 填充的集合。为了在这两个集合之间找到一个二分匹配,我们用最低的代价搜索N个元素 σ ∈ ℘ N \sigma \in {\wp _N} σ∈℘N的一个置换:
σ ^ = arg min σ ∈ ℘ N ∑ i N L m a t c h ( y i , y ^ σ ( i ) ) \hat \sigma = \mathop {\arg \min }\limits_{\sigma \in {\wp _N}} \sum\limits_i^N {{L_{match}}({y_i},{{\hat y}_{\sigma (i)}})} σ^=σ∈℘Nargmini∑NLmatch(yi,y^σ(i))
-
L m a t c h ( y i , y ^ σ ( i ) ) {{L_{match}}({y_i},{{\hat y}_{\sigma (i)}})} Lmatch(yi,y^σ(i))是真值 y i {{y_i}} yi和具有索引 σ i {\sigma _i} σi的一个预测之间的一个成对匹配代价(a pair-wise matching cost)。这个最优分配是通过匈牙利算法计算的。匹配代价同时考虑了类预测以及预测框和真实框之间的相似性。
-
真实集合的每个元素 i i i都可以看成一个 y i = ( c i , b i ) {y_i} = ({c_i},{b_i}) yi=(ci,bi),其中 c i {c_i} ci是目标类标签(目标类标签特可能是 ϕ \phi ϕ)。 b i ∈ [ 0 , 1 ] 4 {b_i} \in {\left[ {0,1} \right]^4} bi∈[0,1]4是一个向量,它定义了真实框的中心坐标及其相对于图像的高度和宽度。
-
对于索引 σ i {\sigma _i} σi的预测,我们定义类 c i {c _i} ci的概率为 p ^ σ ( i ) ( c i ) {{\hat p}_{\sigma (i)}}({c_i}) p^σ(i)(ci),预测框为 b ^ σ ( i ) {{\hat b}_{\sigma (i)}} b^σ(i)。
利用上述的符号,可以将 L m a t c h ( y i , y ^ σ ( i ) ) {{L_{match}}({y_i},{{\hat y}_{\sigma (i)}})} Lmatch(yi,y^σ(i))定义为:
− 1 { c i ≠ ϕ } p ^ σ ( i ) ( c i ) + 1 { c i ≠ ϕ } L b o x ( b i , b ^ σ ( i ) ) - {1_{\{ {c_i} \ne \phi \} }}{{\hat p}_{\sigma (i)}}({c_i}) + {1_{\{ {c_i} \ne \phi \} }}{L_{box}}({b_i},{{\hat b}_{\sigma (i)}}) −1{ci=ϕ}p^σ(i)(ci)+1{ci=ϕ}Lbox(bi,b^σ(i))
其损失函数是计算上一步中匹配的所有配对的匈牙利损失。我们定义的损失类似于常见目标检测器的损失,即类别预测的负对数和box 损失的线性组合:
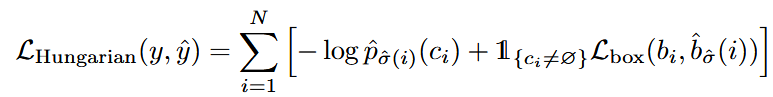
其中的 σ ^ {\hat \sigma } σ^是第一步中计算的最优分配。
1.3 论文中的示例代码
import torch
from torch import nn
from torchvision.models import resnet50
class DETR(nn.Module):
def __init__(self, num_classes, hidden_dim, nheads, num_encoder_layers, num_decoder_layers):
super().__init__()
# backbone = resnet50 除掉average pool和fc层 只保留conv1 - conv5_x
self.backbone = nn.Sequential(*list(resnet50(pretrained=True).children())[:-2])
# 1x1卷积降维 2048->256
self.conv = nn.Conv2d(2048, hidden_dim, 1)
# 6层encoder + 6层decoder hidden_dim=256 nheads多头注意力机制 8头 num_encoder_layers=num_decoder_layers=6
self.transformer = nn.Transformer(hidden_dim, nheads, num_encoder_layers, num_decoder_layers)
# 分类头
self.linear_class = nn.Linear(hidden_dim, num_classes + 1)
# 回归头
self.linear_bbox = nn.Linear(hidden_dim, 4)
# 位置编码 encoder输入
self.row_embed = nn.Parameter(torch.rand(50, hidden_dim // 2))
self.col_embed = nn.Parameter(torch.rand(50, hidden_dim // 2))
# query pos编码 decoder输入
self.query_pos = nn.Parameter(torch.rand(100, hidden_dim))
def forward(self, inputs):
x = self.backbone(inputs) # [1,3,800,1066] -> [1,2048,25,34]
h = self.conv(x) # [1,2048,25,34] -> [1,256,25,34]
H, W = h.shape[-2:] # H=25 W=34
# pos = [850,1,256] self.col_embed = [50,128] self.row_embed[:H]=[50,128]
pos = torch.cat([self.col_embed[:W].unsqueeze(0).repeat(H, 1, 1),
self.row_embed[:H].unsqueeze(1).repeat(1, W, 1),
], dim=-1).flatten(0, 1).unsqueeze(1)
# encoder输入 decoder输入
h = self.transformer(pos + h.flatten(2).permute(2, 0, 1), self.query_pos.unsqueeze(1))
return self.linear_class(h), self.linear_bbox(h).sigmoid()
detr = DETR(num_classes=91, hidden_dim=256, nheads=8, num_encoder_layers=6, num_decoder_layers=6)
detr.eval()
inputs = torch.randn(1, 3, 800, 1066)
logits, bboxes = detr(inputs)
print(logits.shape) # torch.Size([100, 1, 92])
print(bboxes.shape) # torch.Size([100, 1, 4])
论文原文给出的代码,mAP只有40,虽然比真实的源码低了2个点,但是代码很简单,只有40多行,方便我们了解整个DETR的网络结构,可以与上述的DETR框架一一对应起来。
2. Backbone代码
整个Backbone主要包括CNN特征提取和位置编码两个部分。
首先是调用models/Backbone.py中的build_backbone函数创建Backbone:
def build_backbone(args):
# 搭建backbone
# 位置编码 PositionEmbeddingSine()
position_embedding = build_position_encoding(args)
train_backbone = args.lr_backbone > 0 # 是否需要训练backbone True
return_interm_layers = args.masks # 是否需要返回中间层结果 目标检测False 分割True
# 生成backbone resnet50
backbone = Backbone(args.backbone, train_backbone, return_interm_layers, args.dilation)
# 将backbone输出与位置编码相加 0: backbone 1: PositionEmbeddingSine()
model = Joiner(backbone, position_embedding)
model.num_channels = backbone.num_channels # 512
return model
这里首先调用build_position_encoding函数生成正余弦位置编码position_embedding:[bs,256,H/32, W/32],其中256前128是y方向位置编码,后128是x方向位置编码;再调用Backbone类生成ResNet50对输入数据进行特征提取得到特征图[bs,2048,H/32, W/32]。最后Joiner将两者合并存储起来,方便后续使用。
2.1 CNN特征提取部分代码
创建ResNet50,先调用Backbone类:
class Backbone(BackboneBase):
"""ResNet backbone with frozen BatchNorm."""
def __init__(self, name: str,
train_backbone: bool,
return_interm_layers: bool,
dilation: bool):
# 直接调包 调用torchvision.models中的backbone
backbone = getattr(torchvision.models, name)(
replace_stride_with_dilation=[False, False, dilation],
pretrained=is_main_process(), norm_layer=FrozenBatchNorm2d)
# resnet50 2048
num_channels = 512 if name in ('resnet18', 'resnet34') else 2048
super().__init__(backbone, train_backbone, num_channels, return_interm_layers)
这个类是继承自BackboneBase类的,而且CNN直接调用的就是torchvision.models中的模型,所以直接看BackboneBase类:
class BackboneBase(nn.Module):
def __init__(self, backbone: nn.Module, train_backbone: bool, num_channels: int, return_interm_layers: bool):
super().__init__()
for name, parameter in backbone.named_parameters():
# layer0 layer1不需要训练 因为前面层提取的信息其实很有限 都是差不多的 不需要训练
if not train_backbone or 'layer2' not in name and 'layer3' not in name and 'layer4' not in name:
parameter.requires_grad_(False)
# False 检测任务不需要返回中间层
if return_interm_layers:
return_layers = {"layer1": "0", "layer2": "1", "layer3": "2", "layer4": "3"}
else:
return_layers = {'layer4': "0"}
# 检测任务直接返回layer4即可 执行torchvision.models._utils.IntermediateLayerGetter这个函数可以直接返回对应层的输出结果
self.body = IntermediateLayerGetter(backbone, return_layers=return_layers)
self.num_channels = num_channels
def forward(self, tensor_list: NestedTensor):
"""
tensor_list: pad预处理之后的图像信息
tensor_list.tensors: [bs, 3, 608, 810]预处理后的图片数据 对于小图片而言多余部分用0填充
tensor_list.mask: [bs, 608, 810] 用于记录矩阵中哪些地方是填充的(原图部分值为False,填充部分值为True)
"""
# 取出预处理后的图片数据 [bs, 3, 608, 810] 输入模型中 输出layer4的输出结果 dict '0'=[bs, 2048, 19, 26]
xs = self.body(tensor_list.tensors)
# 保存输出数据
out: Dict[str, NestedTensor] = {}
for name, x in xs.items():
m = tensor_list.mask # 取出图片的mask [bs, 608, 810] 知道图片哪些区域是有效的 哪些位置是pad之后的无效的
assert m is not None
# 通过插值函数知道卷积后的特征的mask 知道卷积后的特征哪些是有效的 哪些是无效的
# 因为之前图片输入网络是整个图片都卷积计算的 生成的新特征其中有很多区域都是无效的
mask = F.interpolate(m[None].float(), size=x.shape[-2:]).to(torch.bool)[0]
# out['0'] = NestedTensor: tensors[bs, 2048, 19, 26] + mask[bs, 19, 26]
out[name] = NestedTensor(x, mask)
# out['0'] = NestedTensor: tensors[bs, 2048, 19, 26] + mask[bs, 19, 26]
return out
这个类还是在调用torchvision.models中的模型,然后再把预处理后的图片数据[bs, 3, 608, 810]和mask数据[bs, 608, 810]输入到模型中(这个图片数据是经过pad填充的数据,而mask数据就是记录这些图片哪些像素位置是pad的,为True,没用pad的真实有效数据就为False)。经过前向传播,再调用IntermediateLayerGetter函数把对应层特征图提取出来,得到原图32倍下采样的特征图[bs, 2048, 19, 26],以及这张特征图对应的mask[bs, 19, 26]。
2.2 位置编码部分代码
这里主要是调用models/position_encoding.py中的build_position_encoding函数创建位置编码:
def build_position_encoding(args):
"""
创建位置编码
args: 一系列参数 args.hidden_dim: transformer中隐藏层的维度 args.position_embedding: 位置编码类型 正余弦sine or 可学习learned
"""
# N_steps = 128 = 256 // 2 backbone输出[bs,256,25,34] 256维度的特征
# 而传统的位置编码应该也是256维度的, 但是detr用的是一个x方向和y方向的位置编码concat的位置编码方式 这里和ViT有所不同
# 二维位置编码 前128维代表x方向位置编码 后128维代表y方向位置编码
N_steps = args.hidden_dim // 2
if args.position_embedding in ('v2', 'sine'):
# TODO find a better way of exposing other arguments
# [bs,256,19,26] dim=1时 前128个是y方向位置编码 后128个是x方向位置编码
position_embedding = PositionEmbeddingSine(N_steps, normalize=True)
elif args.position_embedding in ('v3', 'learned'):
position_embedding = PositionEmbeddingLearned(N_steps)
else:
raise ValueError(f"not supported {args.position_embedding}")
return position_embedding
可以看到,源码是实现了两种位置编码,一种是正余弦绝对位置编码,不需要额外的参数学习,另一种是可学习绝对位置编码。原论文用的是正余弦绝对位置编码,而且代码也是默认使用这个的,所以这里主要介绍PositionEmbeddingSine类:
class PositionEmbeddingSine(nn.Module):
"""
Absolute pos embedding, Sine. 没用可学习参数 不可学习 定义好了就固定了
This is a more standard version of the position embedding, very similar to the one
used by the Attention is all you need paper, generalized to work on images.
"""
def __init__(self, num_pos_feats=64, temperature=10000, normalize=False, scale=None):
super().__init__()
self.num_pos_feats = num_pos_feats # 128维度 x/y = d_model/2
self.temperature = temperature # 常数 正余弦位置编码公式里面的10000
self.normalize = normalize # 是否对向量进行max规范化 True
if scale is not None and normalize is False:
raise ValueError("normalize should be True if scale is passed")
if scale is None:
# 这里之所以规范化到2*pi 因为位置编码函数的周期是[2pi, 20000pi]
scale = 2 * math.pi # 规范化参数 2*pi
self.scale = scale
def forward(self, tensor_list: NestedTensor):
x = tensor_list.tensors # [bs, 2048, 19, 26] 预处理后的 经过backbone 32倍下采样之后的数据 对于小图片而言多余部分用0填充
mask = tensor_list.mask # [bs, 19, 26] 用于记录矩阵中哪些地方是填充的(原图部分值为False,填充部分值为True)
assert mask is not None
not_mask = ~mask # True的位置才是真实有效的位置
# 考虑到图像本身是2维的 所以这里使用的是2维的正余弦位置编码
# 这样各行/列都映射到不同的值 当然有效位置是正常值 无效位置会有重复值 但是后续计算注意力权重会忽略这部分的
# 而且最后一个数字就是有效位置的总和,方便max规范化
# 计算此时y方向上的坐标 [bs, 19, 26]
y_embed = not_mask.cumsum(1, dtype=torch.float32)
# 计算此时x方向的坐标 [bs, 19, 26]
x_embed = not_mask.cumsum(2, dtype=torch.float32)
# 最大值规范化 除以最大值 再乘以2*pi 最终把坐标规范化到0-2pi之间
if self.normalize:
eps = 1e-6
y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale
dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device) # 0 1 2 .. 127
# 2i/2i+1: 2 * (dim_t // 2) self.temperature=10000 self.num_pos_feats = d/2
dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats) # 分母
pos_x = x_embed[:, :, :, None] / dim_t # 正余弦括号里面的公式
pos_y = y_embed[:, :, :, None] / dim_t # 正余弦括号里面的公式
# x方向位置编码: [bs,19,26,64][bs,19,26,64] -> [bs,19,26,64,2] -> [bs,19,26,128]
pos_x = torch.stack((pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4).flatten(3)
# y方向位置编码: [bs,19,26,64][bs,19,26,64] -> [bs,19,26,64,2] -> [bs,19,26,128]
pos_y = torch.stack((pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4).flatten(3)
# concat: [bs,19,26,128][bs,19,26,128] -> [bs,19,26,256] -> [bs,256,19,26]
pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
# [bs,256,19,26] dim=1时 前128个是y方向位置编码 后128个是x方向位置编码
return pos
可以对照公式:
P E ( p o s , 2 i ) = sin ( p o s / 1000 0 2 i / d m o d e l ) P{E_{(pos,2i)}} = \sin (pos/{10000^{2i/{d_{\bmod el}}}}) PE(pos,2i)=sin(pos/100002i/dmodel)
P E ( p o s , 2 i + 1 ) = cos ( p o s / 1000 0 2 i / d m o d e l ) P{E_{(pos,2i + 1)}} = \cos (pos/{10000^{2i/{d_{\bmod el}}}}) PE(pos,2i+1)=cos(pos/100002i/dmodel)
3. Transfomer代码
先看下调用接口:
def build_transformer(args):
return Transformer(
d_model=args.hidden_dim,
dropout=args.dropout,
nhead=args.nheads,
dim_feedforward=args.dim_feedforward,
num_encoder_layers=args.enc_layers,
num_decoder_layers=args.dec_layers,
normalize_before=args.pre_norm,
return_intermediate_dec=True,
)
直接调用Transformer类:
class Transformer(nn.Module):
def __init__(self, d_model=512, nhead=8, num_encoder_layers=6,
num_decoder_layers=6, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False,
return_intermediate_dec=False):
super().__init__()
"""
d_model: 编码器里面mlp(前馈神经网络 2个linear层)的hidden dim 512
nhead: 多头注意力头数 8
num_encoder_layers: encoder的层数 6
num_decoder_layers: decoder的层数 6
dim_feedforward: 前馈神经网络的维度 2048
dropout: 0.1
activation: 激活函数类型 relu
normalize_before: 是否使用前置LN
return_intermediate_dec: 是否返回decoder中间层结果 False
"""
# 初始化一个小encoder
encoder_layer = TransformerEncoderLayer(d_model, nhead, dim_feedforward,
dropout, activation, normalize_before)
encoder_norm = nn.LayerNorm(d_model) if normalize_before else None
# 创建整个Encoder层 6个encoder层堆叠
self.encoder = TransformerEncoder(encoder_layer, num_encoder_layers, encoder_norm)
# 初始化一个小decoder
decoder_layer = TransformerDecoderLayer(d_model, nhead, dim_feedforward,
dropout, activation, normalize_before)
decoder_norm = nn.LayerNorm(d_model)
# 创建整个Decoder层 6个decoder层堆叠
self.decoder = TransformerDecoder(decoder_layer, num_decoder_layers, decoder_norm,
return_intermediate=return_intermediate_dec)
# 参数初始化
self._reset_parameters()
self.d_model = d_model # 编码器里面mlp的hidden dim 512
self.nhead = nhead # 多头注意力头数 8
def _reset_parameters(self):
for p in self.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
def forward(self, src, mask, query_embed, pos_embed):
"""
src: [bs,256,19,26] 图片输入backbone+1x1conv之后的特征图
mask: [bs, 19, 26] 用于记录特征图中哪些地方是填充的(原图部分值为False,填充部分值为True)
query_embed: [100, 256] 类似于传统目标检测里面的anchor 这里设置了100个 需要预测的目标
pos_embed: [bs, 256, 19, 26] 位置编码
"""
# bs c=256 h=19 w=26
bs, c, h, w = src.shape
# src: [bs,256,19,26]=[bs,C,H,W] -> [494,bs,256]=[HW,bs,C]
src = src.flatten(2).permute(2, 0, 1)
# pos_embed: [bs, 256, 19, 26]=[bs,C,H,W] -> [494,bs,256]=[HW,bs,C]
pos_embed = pos_embed.flatten(2).permute(2, 0, 1)
# query_embed: [100, 256]=[num,C] -> [100,bs,256]=[num,bs,256]
query_embed = query_embed.unsqueeze(1).repeat(1, bs, 1)
# mask: [bs, 19, 26]=[bs,H,W] -> [bs,494]=[bs,HW]
mask = mask.flatten(1)
# tgt: [100, bs, 256] 需要预测的目标query embedding 和 query_embed形状相同 且全设置为0
# 在每层decoder层中不断的被refine,相当于一次次的被coarse-to-fine的过程
tgt = torch.zeros_like(query_embed)
# memory: [494, bs, 256]=[HW, bs, 256] Encoder输出 具有全局相关性(增强后)的特征表示
memory = self.encoder(src, src_key_padding_mask=mask, pos=pos_embed)
# [6, 100, bs, 256]
# tgt:需要预测的目标 query embeding
# memory: encoder的输出
# pos: memory的位置编码
# query_pos: tgt的位置编码
hs = self.decoder(tgt, memory, memory_key_padding_mask=mask,
pos=pos_embed, query_pos=query_embed)
# decoder输出 [6, 100, bs, 256] -> [6, bs, 100, 256]
# encoder输出 [bs, 256, H, W]
return hs.transpose(1, 2), memory.permute(1, 2, 0).view(bs, c, h, w)
仔细分析这个类会发现,我们虽然暂时不了解模型的细节部分,但是模型的主体框架已经定义出来了。整个Transformer其实就是输入经过Backbone输出的特征图src(降维到256)、src_key_padding_mask(记录特征图每个位置是否是被pad的,pad的就不需要计算注意力)和位置编码pos到TransformerEncoder中,而TransformerEncoder其实是由TransformerEncoderLayer组成的;然后再输入encoder的输出、mask、位置编码和query编码到TransformerEncoder中,而TransformerEncoder是由TransformerDecoderLayer组成的。
所以,下面分为TransformerEncoder和TransformerDecoder两个模块来了解Transformer具体细节组成。
3.1 TransformerEncoder代码
这个部分就是调用_get_clones函数,复制6份TransformerEncoderLayer类,然后前向传播依次输入这6个TransformerEncoderLayer类,不断的计算特征图的自注意力,并不断的增强特征图,最终得到最强的(信息最多的)特征图output:[h*w, bs, 256]。值得注意的是,整个TransformerEncoder过程特征图的shape是不变的。
class TransformerEncoder(nn.Module):
def __init__(self, encoder_layer, num_layers, norm=None):
super().__init__()
# 复制num_layers=6份encoder_layer=TransformerEncoderLayer
self.layers = _get_clones(encoder_layer, num_layers)
# 6层TransformerEncoderLayer
self.num_layers = num_layers
self.norm = norm # layer norm
def forward(self, src,
mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
"""
src: [h*w, bs, 256] 经过Backbone输出的特征图(降维到256)
mask: None
src_key_padding_mask: [h*w, bs] 记录每个特征图的每个位置是否是被pad的(True无效 False有效)
pos: [h*w, bs, 256] 每个特征图的位置编码
"""
output = src
# 遍历这6层TransformerEncoderLayer
for layer in self.layers:
output = layer(output, src_mask=mask,
src_key_padding_mask=src_key_padding_mask, pos=pos)
if self.norm is not None:
output = self.norm(output)
# 得到最终ENCODER的输出 [h*w, bs, 256]
return output
def _get_clones(module, N):
return nn.ModuleList([copy.deepcopy(module) for i in range(N)])
我们来看一下TransformerEncoderLayer:
下图是TransformerEncoderLayer的结构:Encoder Layer = multi-head Attention + add&Norm + feed forward + add&Norm,重点在于multi-head Attention。

class TransformerEncoderLayer(nn.Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False):
super().__init__()
"""
小encoder层 结构:multi-head Attention + add&Norm + feed forward + add&Norm
d_model: mlp 前馈神经网络的dim
nhead: 8头注意力机制
dim_feedforward: 前馈神经网络的维度 2048
dropout: 0.1
activation: 激活函数类型
normalize_before: 是否使用先LN False
"""
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Implementation of Feedforward model
self.linear1 = nn.Linear(d_model, dim_feedforward)
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(dim_feedforward, d_model)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.activation = _get_activation_fn(activation)
self.normalize_before = normalize_before
def with_pos_embed(self, tensor, pos: Optional[Tensor]):
# 这个操作是把词向量和位置编码相加操作
return tensor if pos is None else tensor + pos
def forward_post(self,
src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
"""
src: [494, bs, 256] backbone输入下采样32倍后 再 压缩维度到256的特征图
src_mask: None
src_key_padding_mask: [bs, 494] 记录哪些位置有pad True 没意义 不需要计算attention
pos: [494, bs, 256] 位置编码
"""
# 数据 + 位置编码 [494, bs, 256]
# 这也是和原版encoder不同的地方,这里每个encoder的q和k都会加上位置编码 再用q和k计算相似度 再和v加权得到更具有全局相关性(增强后)的特征表示
# 每用一层都加上位置编码 信息不断加强 最终得到的特征全局相关性最强 原版的transformer只在输入加上位置编码 作者发现这样更好
q = k = self.with_pos_embed(src, pos)
# multi-head attention [494, bs, 256]
# q 和 k = backbone输出特征图 + 位置编码
# v = backbone输出特征图
# 这里对query和key增加位置编码 是因为需要在图像特征中各个位置之间计算相似度/相关性 而value作为原图像的特征 和 相关性矩阵加权,
# 从而得到各个位置结合了全局相关性(增强后)的特征表示,所以q 和 k这种计算需要+位置编码 而v代表原图像不需要加位置编码
# nn.MultiheadAttention: 返回两个值 第一个是自注意力层的输出 第二个是自注意力权重 这里取0
# key_padding_mask: 记录backbone生成的特征图中哪些是原始图像pad的部分 这部分是没有意义的
# 计算注意力会被填充为-inf,这样最终生成注意力经过softmax时输出就趋向于0,相当于忽略不计
# attn_mask: 是在Transformer中用来“防作弊”的,即遮住当前预测位置之后的位置,忽略这些位置,不计算与其相关的注意力权重
# 而在encoder中通常为None 不适用 decoder中才使用
src2 = self.self_attn(q, k, value=src, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)[0]
# add + norm + feed forward + add + norm
src = src + self.dropout1(src2)
src = self.norm1(src)
src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
src = src + self.dropout2(src2)
src = self.norm2(src)
return src
def forward_pre(self, src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
src2 = self.norm1(src)
q = k = self.with_pos_embed(src2, pos)
src2 = self.self_attn(q, k, value=src2, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)[0]
src = src + self.dropout1(src2)
src2 = self.norm2(src)
src2 = self.linear2(self.dropout(self.activation(self.linear1(src2))))
src = src + self.dropout2(src2)
return src
def forward(self, src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
if self.normalize_before: # False
return self.forward_pre(src, src_mask, src_key_padding_mask, pos)
return self.forward_post(src, src_mask, src_key_padding_mask, pos) # 默认执行
有几个很关键的点(和原始transformer encoder不同的地方):
- 为什么每个encoder的q和k都是+位置编码的?
如果学过transformer的知道,通常都是在transformer的输入加上位置编码,而每个encoder的qkv都是相等的,都是不加位置编码的。而这里先将q和k都会加上位置编码,再用q和k计算相似度,最后和v加权得到更具有全局相关性(增强后)的特征表示。每一层都加上位置编码,每一层全局信息不断加强,最终可以得到最强的全局特征。
- 为什么q和k+位置编码,而v不需要加上位置编码?
因为q和k是用来计算图像特征中各个位置之间计算相似度/相关性的,加上位置编码后计算出来的全局特征相关性更强,而v代表原图像,所以并不需要加位置编码。
3.2 TransformerDecoder代码
Decoder结构和Encoder的结构类似,也是用_get_clones复制6份TransformerDecoderLayer类,然后前向传播依次输入这6个TransformerDecoderLayer类,不过不同的,Decoder需要输入这6个TransformerDecoderLayer的输出,后面这6个层的输出会一起参与损失计算。
class TransformerDecoder(nn.Module):
def __init__(self, decoder_layer, num_layers, norm=None, return_intermediate=False):
super().__init__()
# 复制num_layers=decoder_layer=TransformerDecoderLayer
self.layers = _get_clones(decoder_layer, num_layers)
self.num_layers = num_layers # 6
self.norm = norm # LN
# 是否返回中间层 默认True 因为DETR默认6个Decoder都会返回结果,一起加入损失计算的
# 每一层Decoder都是逐层解析,逐层加强的,所以前面层的解析效果对后面层的解析是有意义的,所以作者把前面5层的输出也加入损失计算
self.return_intermediate = return_intermediate
def forward(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
"""
tgt: [100, bs, 256] 需要预测的目标query embedding 和 query_embed形状相同 且全设置为0
在每层decoder层中不断的被refine,相当于一次次的被coarse-to-fine的过程
memory: [h*w, bs, 256] Encoder输出 具有全局相关性(增强后)的特征表示
tgt_mask: None
tgt_key_padding_mask: None
memory_key_padding_mask: [bs, h*w] 记录Encoder输出特征图的每个位置是否是被pad的(True无效 False有效)
pos: [h*w, bs, 256] 特征图的位置编码
query_pos: [100, bs, 256] query embedding的位置编码 随机初始化的
"""
output = tgt # 初始化query embedding 全是0
intermediate = [] # 用于存放6层decoder的输出结果
# 遍历6层decoder
for layer in self.layers:
output = layer(output, memory, tgt_mask=tgt_mask,
memory_mask=memory_mask,
tgt_key_padding_mask=tgt_key_padding_mask,
memory_key_padding_mask=memory_key_padding_mask,
pos=pos, query_pos=query_pos)
# 6层结果全部加入intermediate
if self.return_intermediate:
intermediate.append(self.norm(output))
if self.norm is not None:
output = self.norm(output)
if self.return_intermediate:
intermediate.pop()
intermediate.append(output)
# 默认执行这里
# 最后把 6x[100,bs,256] -> [6(6层decoder输出),100,bs,256]
if self.return_intermediate:
return torch.stack(intermediate)
return output.unsqueeze(0) # 不执行
我们来看一下TransformerDecoderLayer:
下图是TransformerDecoderLayer的结构:decoder layer = Masked Multi-Head Attention + Add&Norm + Multi-Head Attention + add&Norm + feed forward + add&Norm。关键点在于两个Attention层,搞懂这两层的原理、区别是理解Decoder的关键。
class TransformerDecoderLayer(nn.Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False):
super().__init__()
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
self.multihead_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Implementation of Feedforward model
self.linear1 = nn.Linear(d_model, dim_feedforward)
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(dim_feedforward, d_model)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.norm3 = nn.LayerNorm(d_model)
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.dropout3 = nn.Dropout(dropout)
self.activation = _get_activation_fn(activation)
self.normalize_before = normalize_before
def with_pos_embed(self, tensor, pos: Optional[Tensor]):
return tensor if pos is None else tensor + pos
def forward_post(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
"""
tgt: 需要预测的目标 query embedding 负责预测物体 用于建模图像当中的物体信息 在每层decoder层中不断的被refine
[100, bs, 256] 和 query_embed形状相同 且全设置为0
memory: [h*w, bs, 256] Encoder输出 具有全局相关性(增强后)的特征表示
tgt_mask: None
memory_mask: None
tgt_key_padding_mask: None
memory_key_padding_mask: [bs, h*w] 记录Encoder输出特征图的每个位置是否是被pad的(True无效 False有效)
pos: [h*w, bs, 256] encoder输出特征图的位置编码
query_pos: [100, bs, 256] query embedding/tgt的位置编码 负责建模物体与物体之间的位置关系 随机初始化的
tgt_mask、memory_mask、tgt_key_padding_mask是防止作弊的 这里都没有使用
"""
# 第一个self-attention的目的:找到图像中物体的信息 -> tgt
# 第一个多头自注意力层:输入qkv都和Encoder无关 都来自于tgt/query embedding
# 通过第一个self-attention 可以不断建模物体与物体之间的关系 可以知道图像当中哪些位置会存在物体 物体信息->tgt
# query embedding + query_pos
q = k = self.with_pos_embed(tgt, query_pos)
# masked multi-head self-attention 计算query embedding的自注意力
tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask)[0]
# add + norm
tgt = tgt + self.dropout1(tgt2)
tgt = self.norm1(tgt)
# 第二个self-attention的目的:不断增强encoder的输出特征,将物体的信息不断加入encoder的输出特征中去,更好地表征了图像中的各个物体
# 第二个多头注意力层,也叫Encoder-Decoder self attention:key和value来自Encoder层输出 Query来自Decoder层输入
# 第二个self-attention 可以建模图像 与 物体之间的关系
# 根据上一步得到的tgt作为query 不断的去encoder输出的特征图中去问(q和k计算相似度) 问图像当中的物体在哪里呢?
# 问完之后再将物体的位置信息融合encoder输出的特征图中(和v做运算) 这样我得到的v的特征就有 encoder增强后特征信息 + 物体的位置信息
# query = query embedding + query_pos
# key = encoder输出特征 + 特征位置编码
# value = encoder输出特征
tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos),
key=self.with_pos_embed(memory, pos),
value=memory, attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask)[0]
# ada + norm + Feed Forward + add + norm
tgt = tgt + self.dropout2(tgt2)
tgt = self.norm2(tgt)
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
tgt = tgt + self.dropout3(tgt2)
tgt = self.norm3(tgt)
# [100, bs, 256]
# decoder的输出是第一个self-attention输出特征 + 第二个self-attention输出特征
# 最终的特征:知道图像中物体与物体之间的关系 + encoder增强后的图像特征 + 图像与物体之间的关系
return tgt
def forward_pre(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
tgt2 = self.norm1(tgt)
q = k = self.with_pos_embed(tgt2, query_pos)
tgt2 = self.self_attn(q, k, value=tgt2, attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask)[0]
tgt = tgt + self.dropout1(tgt2)
tgt2 = self.norm2(tgt)
tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt2, query_pos),
key=self.with_pos_embed(memory, pos),
value=memory, attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask)[0]
tgt = tgt + self.dropout2(tgt2)
tgt2 = self.norm3(tgt)
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt2))))
tgt = tgt + self.dropout3(tgt2)
return tgt
def forward(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
if self.normalize_before:
return self.forward_pre(tgt, memory, tgt_mask, memory_mask,
tgt_key_padding_mask, memory_key_padding_mask, pos, query_pos)
return self.forward_post(tgt, memory, tgt_mask, memory_mask,
tgt_key_padding_mask, memory_key_padding_mask, pos, query_pos)
Decoder的主要作用:
- 从Encoder的最终输出,我们得到了增强版的图像特征memory,以及特征的位置信息pos。
- 自定义了图像当中的物体信息tgt,初始化为全0,以及图像中的物体位置信息query_pos,随机初始化。
- 第一个self-attention:qk=tgt+query_pos,v=tgt,计算图像中物体与物体的相关性,负责建模图像中的物体信息,最终得到的tgt1,是增强版的物体信息,这些位置信息包含了物体与物体之间的位置关系。
- 第二个self-attention:q=tgt+qyery_pos,k=memory+pos,v=memory,以物体的信息tgt作为query,去图像特征memory中去问(计算他们的相关性),问图像中物体在哪里呢?问完之后再将物体的位置信息融入到图像特征中去(v),整个过程是负责建模图像特征与物体特征之间的关系,最后得到的是更强的图像特征tgt2,包括encoder输出的增强版的图像特征+物体的位置特征。
- 最后把tgt1 + tgt2 = Encoder输出的增强版图像特征 + 物体信息 + 物体位置信息,作为decoder的输出。
4. 损失计算代码
首先在detr.py中会先定义好损失函数:
criterion = SetCriterion(num_classes, matcher=matcher, weight_dict=weight_dict,eos_coef=args.eos_coef, losses=losses)
criterion.to(device)
然后在engine.py的train_one_epoch中前向推理结束后调用criterion函数,计算损失:
# 前向传播
outputs = model(samples)
# 计算损失 loss_dict: 'loss_ce' + 'loss_bbox' + 'loss_giou' 用于log日志: 'class_error' + 'cardinality_error'
loss_dict = criterion(outputs, targets)
# 权重系数 {'loss_ce': 1, 'loss_bbox': 5, 'loss_giou': 2}
weight_dict = criterion.weight_dict
# 总损失 = 回归损失:loss_bbox(L1)+loss_bbox + 分类损失:loss_ce
losses = sum(loss_dict[k] * weight_dict[k] for k in loss_dict.keys() if k in weight_dict)
SetCriterion类的内容为:
class SetCriterion(nn.Module):
""" This class computes the loss for DETR.
The process happens in two steps:
1) we compute hungarian assignment between ground truth boxes and the outputs of the model
2) we supervise each pair of matched ground-truth / prediction (supervise class and box)
"""
def __init__(self, num_classes, matcher, weight_dict, eos_coef, losses):
""" Create the criterion.
Parameters:
num_classes: number of object categories, omitting the special no-object category
matcher: module able to compute a matching between targets and proposals
weight_dict: dict containing as key the names of the losses and as values their relative weight.
eos_coef: relative classification weight applied to the no-object category
losses: list of all the losses to be applied. See get_loss for list of available losses.
"""
super().__init__()
self.num_classes = num_classes # 数据集类别数
self.matcher = matcher # HungarianMatcher() 匈牙利算法 二分图匹配
self.weight_dict = weight_dict # dict: 18 3x6 6个decoder的损失权重 6*(loss_ce+loss_giou+loss_bbox)
self.eos_coef = eos_coef # 0.1
self.losses = losses # list: 3 ['labels', 'boxes', 'cardinality']
empty_weight = torch.ones(self.num_classes + 1)
empty_weight[-1] = self.eos_coef # tensro: 92 前91=1 92=eos_coef=0.1
self.register_buffer('empty_weight', empty_weight)
def forward(self, outputs, targets):
""" This performs the loss computation.
Parameters:
outputs: dict of tensors, see the output specification of the model for the format
dict: 'pred_logits'=Tensor[bs, 100, 92个class] 'pred_boxes'=Tensor[bs, 100, 4] 最后一个decoder层输出
'aux_output'={list:5} 0-4 每个都是dict:2 pred_logits+pred_boxes 表示5个decoder前面层的输出
targets: list of dicts, such that len(targets) == batch_size. list: bs
每张图片包含以下信息:'boxes'、'labels'、'image_id'、'area'、'iscrowd'、'orig_size'、'size'
The expected keys in each dict depends on the losses applied, see each loss' doc
"""
# dict: 2 最后一个decoder层输出 pred_logits[bs, 100, 92个class] + pred_boxes[bs, 100, 4]
outputs_without_aux = {k: v for k, v in outputs.items() if k != 'aux_outputs'}
# 匈牙利算法 解决二分图匹配问题 从100个预测框中找到和N个gt框一一对应的预测框 其他的100-N个都变为背景
# Retrieve the matching between the outputs of the last layer and the targets list:1
# tuple: 2 0=Tensor3=Tensor[5, 35, 63] 匹配到的3个预测框 其他的97个预测框都是背景
# 1=Tensor3=Tensor[1, 0, 2] 对应的三个gt框
indices = self.matcher(outputs_without_aux, targets)
# Compute the average number of target boxes accross all nodes, for normalization purposes
num_boxes = sum(len(t["labels"]) for t in targets) # int 统计这整个batch的所有图片的gt总个数 3
num_boxes = torch.as_tensor([num_boxes], dtype=torch.float, device=next(iter(outputs.values())).device)
if is_dist_avail_and_initialized():
torch.distributed.all_reduce(num_boxes)
num_boxes = torch.clamp(num_boxes / get_world_size(), min=1).item() # 3.0
# 计算最后层decoder损失 Compute all the requested losses
losses = {}
for loss in self.losses:
losses.update(self.get_loss(loss, outputs, targets, indices, num_boxes))
# 计算前面5层decoder损失 累加到一起 得到最终的losses
# In case of auxiliary losses, we repeat this process with the output of each intermediate layer.
if 'aux_outputs' in outputs:
for i, aux_outputs in enumerate(outputs['aux_outputs']):
indices = self.matcher(aux_outputs, targets) # 同样匈牙利算法匹配
for loss in self.losses: # 计算各个loss
if loss == 'masks':
# Intermediate masks losses are too costly to compute, we ignore them.
continue
kwargs = {}
if loss == 'labels':
# Logging is enabled only for the last layer
kwargs = {'log': False}
l_dict = self.get_loss(loss, aux_outputs, targets, indices, num_boxes, **kwargs)
l_dict = {k + f'_{i}': v for k, v in l_dict.items()}
losses.update(l_dict)
# 参加权重更新的损失:losses: 'loss_ce' + 'loss_bbox' + 'loss_giou' 用于log日志: 'class_error' + 'cardinality_error'
return losses
整个函数主要在做两件事:
- 调用self.matcher函数,从100个预测框中匹配出N个(gt个数)真正的预测框,匹配出每个gt框对应的预测框。
- 调用self.get_loss函数,计算各个损失。
4.1 self.matcher函数
self.matcher函数就是二分图匹配的过程(匈牙利算法),DETR是在models/matcher.py中的HungarianMatcher类实现了匈牙利匹配算法:
class HungarianMatcher(nn.Module):
"""This class computes an assignment between the targets and the predictions of the network
For efficiency reasons, the targets don't include the no_object. Because of this, in general,
there are more predictions than targets. In this case, we do a 1-to-1 matching of the best predictions,
while the others are un-matched (and thus treated as non-objects).
"""
def __init__(self, cost_class: float = 1, cost_bbox: float = 1, cost_giou: float = 1):
"""Creates the matcher
Params:
cost_class: This is the relative weight of the classification error in the matching cost
cost_bbox: This is the relative weight of the L1 error of the bounding box coordinates in the matching cost
cost_giou: This is the relative weight of the giou loss of the bounding box in the matching cost
"""
super().__init__()
self.cost_class = cost_class
self.cost_bbox = cost_bbox
self.cost_giou = cost_giou
assert cost_class != 0 or cost_bbox != 0 or cost_giou != 0, "all costs cant be 0"
# 不需要更新梯度 只是一种匹配方式
@torch.no_grad()
def forward(self, outputs, targets):
""" Performs the matching
Params:
outputs: This is a dict that contains at least these entries:
"pred_logits": Tensor of dim [batch_size, num_queries, num_classes]=[bs,100,92] with the classification logits
"pred_boxes": Tensor of dim [batch_size, num_queries, 4]=[bs,100,4] with the predicted box coordinates
targets: list:bs This is a list of targets (len(targets) = batch_size), where each target is a dict containing:
"labels": Tensor of dim [num_target_boxes]=[3] (where num_target_boxes is the number of ground-truth
objects in the target) containing the class labels
"boxes": Tensor of dim [num_target_boxes, 4] containing the target box coordinates
Returns:
A list of size batch_size, containing tuples of (index_i, index_j) where:
- index_i is the indices of the selected predictions (in order)
- index_j is the indices of the corresponding selected targets (in order)
For each batch element, it holds:
len(index_i) = len(index_j) = min(num_queries, num_target_boxes)
"""
# batch_size 100
bs, num_queries = outputs["pred_logits"].shape[:2]
# We flatten to compute the cost matrices in a batch
# [2,100,92] -> [200, 92] -> [200, 92]概率
out_prob = outputs["pred_logits"].flatten(0, 1).softmax(-1) # [batch_size * num_queries, num_classes]
# [2,100,4] -> [200, 4]
out_bbox = outputs["pred_boxes"].flatten(0, 1) # [batch_size * num_queries, 4]
# Also concat the target labels and boxes
# [3] idx = 32, 1, 85 concat all labels
tgt_ids = torch.cat([v["labels"] for v in targets])
# [3, 4] concat all box
tgt_bbox = torch.cat([v["boxes"] for v in targets])
# 计算损失 分类 + L1 box + GIOU box
# Compute the classification cost. Contrary to the loss, we don't use the NLL,
# but approximate it in 1 - proba[target class].
# The 1 is a constant that doesn't change the matching, it can be ommitted.
cost_class = -out_prob[:, tgt_ids]
# Compute the L1 cost between boxes
cost_bbox = torch.cdist(out_bbox, tgt_bbox, p=1)
# Compute the giou cost betwen boxes
cost_giou = -generalized_box_iou(box_cxcywh_to_xyxy(out_bbox), box_cxcywh_to_xyxy(tgt_bbox))
# Final cost matrix [100, 3] bs*100个预测框分别和3个gt框的损失矩阵
C = self.cost_bbox * cost_bbox + self.cost_class * cost_class + self.cost_giou * cost_giou
C = C.view(bs, num_queries, -1).cpu() # [bs, 100, 3]
sizes = [len(v["boxes"]) for v in targets] # gt个数 3
# 匈牙利算法进行二分图匹配 从100个预测框中挑选出最终的3个预测框 分别和gt计算损失 这个组合的总损失是最小的
# 0: [3] 5, 35, 63 匹配到的gt个预测框idx
# 1: [3] 1, 0, 2 对应的gt idx
indices = [linear_sum_assignment(c[i]) for i, c in enumerate(C.split(sizes, -1))]
# list: bs 返回bs张图片的匹配结果
# 每张图片都是一个tuple:2
# 0 = Tensor[gt_num,] 匹配到的正样本idx 1 = Tensor[gt_num,] gt的idx
return [(torch.as_tensor(i, dtype=torch.int64), torch.as_tensor(j, dtype=torch.int64)) for i, j in indices]
其实就是先计算每个预测框(100个)和每个gt框的总损失,形成损失矩阵C,然后调用scipy.optimize.linear_sum_assignment写好的匈牙利算法,匹配的原则就是 ”loss总和“ 最小(这里的loss并不是真正的loss,这里只是一种度量方式,和loss的计算方式是不一样的),得到每个gt对应的唯一负责的预测框,其他的预测框会自动归为背景。
linear_sum_assignment,输入一个二分图的度量矩阵(cost 矩阵),计算这个二分图的度量矩阵的最小权重分配方式,返回的是匹配方案对应的矩阵行索引(预测框idx)和列索引(gt框idx)。
4.2 self.get_loss函数
self.get_loss是SetCriterion类定义的一个函数:
def get_loss(self, loss, outputs, targets, indices, num_boxes, **kwargs):
loss_map = {
'labels': self.loss_labels,
'cardinality': self.loss_cardinality,
'boxes': self.loss_boxes,
'masks': self.loss_masks
}
assert loss in loss_map, f'do you really want to compute {loss} loss?'
return loss_map[loss](outputs, targets, indices, num_boxes, **kwargs)
同时会调用分类损失(self.loss_labels)、回归损失(self.boxes)和cardinality损失。不过cardinality损失只用于log,并不参与梯度更新,所以这里不展开叙述,这里重点介绍分类损失和回归损失。
分类损失self.loss_labels:
def loss_labels(self, outputs, targets, indices, num_boxes, log=True):
"""Classification loss (NLL)
targets dicts must contain the key "labels" containing a tensor of dim [nb_target_boxes]
outputs:'pred_logits'=[bs, 100, 92] 'pred_boxes'=[bs, 100, 4] 'aux_outputs'=5*([bs, 100, 92]+[bs, 100, 4])
targets:'boxes'=[3,4] labels=[3] ...
indices: [3] 如:5,35,63 匹配好的3个预测框idx
num_boxes:当前batch的所有gt个数
"""
assert 'pred_logits' in outputs
src_logits = outputs['pred_logits'] # 分类:[bs, 100, 92类别]
# idx tuple:2 0=[num_all_gt] 记录每个gt属于哪张图片 1=[num_all_gt] 记录每个匹配到的预测框的index
idx = self._get_src_permutation_idx(indices)
target_classes_o = torch.cat([t["labels"][J] for t, (_, J) in zip(targets, indices)])
target_classes = torch.full(src_logits.shape[:2], self.num_classes,
dtype=torch.int64, device=src_logits.device)
# 正样本+负样本 上面匹配到的预测框作为正样本 正常的idx 而100个中没有匹配到的预测框作为负样本(idx=91 背景类)
target_classes[idx] = target_classes_o
# 分类损失 = 正样本 + 负样本
loss_ce = F.cross_entropy(src_logits.transpose(1, 2), target_classes, self.empty_weight)
losses = {'loss_ce': loss_ce}
# 日志 记录Top-1精度
if log:
# TODO this should probably be a separate loss, not hacked in this one here
losses['class_error'] = 100 - accuracy(src_logits[idx], target_classes_o)[0]
# losses: 'loss_ce': 分类损失
# 'class_error':Top-1精度 即预测概率最大的那个类别与对应被分配的GT类别是否一致 这部分仅用于日志显示 并不参与模型训练
return losses
def _get_src_permutation_idx(self, indices):
# permute predictions following indices
# [num_all_gt] 记录每个gt都是来自哪张图片的 idx
batch_idx = torch.cat([torch.full_like(src, i) for i, (src, _) in enumerate(indices)])
# 记录匹配到的预测框的idx
src_idx = torch.cat([src for (src, _) in indices])
return batch_idx, src_idx
上述代码总结为:
- 分类损失 = 交叉熵损失。
- 正样本+负样本=100,正样本个数=GT个数,负样本个数=100-GT个数。
- 92个类别,idx=91表示背景类别。
- 注意这里有一个_get_src_permutation_id函数,主要是讲预测框拉平,原本是有batch这个维度的,现在拉平到一维,方便后续计算损失。
- 这里还会计算一个class_error:Top-1精度,用于日志显示。
回归损失self.boxes:
def loss_boxes(self, outputs, targets, indices, num_boxes):
"""Compute the losses related to the bounding boxes, the L1 regression loss and the GIoU loss
targets dicts must contain the key "boxes" containing a tensor of dim [nb_target_boxes, 4]
The target boxes are expected in format (center_x, center_y, w, h), normalized by the image size.
outputs:'pred_logits'=[bs, 100, 92] 'pred_boxes'=[bs, 100, 4] 'aux_outputs'=5*([bs, 100, 92]+[bs, 100, 4])
targets:'boxes'=[3,4] labels=[3] ...
indices: [3] 如:5,35,63 匹配好的3个预测框idx
num_boxes:当前batch的所有gt个数
"""
assert 'pred_boxes' in outputs
# idx tuple:2 0=[num_all_gt] 记录每个gt属于哪张图片 1=[num_all_gt] 记录每个匹配到的预测框的index
idx = self._get_src_permutation_idx(indices)
# [all_gt_num, 4] 这个batch的所有正样本的预测框坐标
src_boxes = outputs['pred_boxes'][idx]
# [all_gt_num, 4] 这个batch的所有gt框坐标
target_boxes = torch.cat([t['boxes'][i] for t, (_, i) in zip(targets, indices)], dim=0)
# 计算L1损失
loss_bbox = F.l1_loss(src_boxes, target_boxes, reduction='none')
losses = {}
losses['loss_bbox'] = loss_bbox.sum() / num_boxes
# 计算GIOU损失
loss_giou = 1 - torch.diag(box_ops.generalized_box_iou(
box_ops.box_cxcywh_to_xyxy(src_boxes),
box_ops.box_cxcywh_to_xyxy(target_boxes)))
losses['loss_giou'] = loss_giou.sum() / num_boxes
# 'loss_bbox': L1回归损失 'loss_giou': giou回归损失
return losses
上述代码可总结为:
- 回归损失:只计算所有正样本的回归损失。
- 回归损失 = L1 Loss + GIOU Loss。
至此介绍完了DETR代码中的大部分内容了。
总结
通过对DETR代码的解读,进一步理解了其创新性和实现细节,代码详细展示了三部分,第一步部分是backbone,包含CNN特征和位置编码Positional Encoding的实现;第二部分是Transformer的实现,主要学习DETR中TransformerEncoderLayer和TransformerDecoderLayer的实现,第三部分是损失函数的实现,学习率匈牙利算法和二分图匹配(self.matcher)的内容。

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献13条内容
已为社区贡献13条内容







所有评论(0)