创建时间：2024-11-28
首发时间：2024-12-04
最后编辑时间：2024-12-04
作者：Geeker_LStar

你好呀~这里是 Geeker_LStar 的人工智能学习专栏，很高兴遇见你~
我是 Geeker_LStar，一名高一学生，热爱计算机和数学，我们一起加油~！
⭐(●’◡’●) ⭐

诶嘿！我又来啦~！

前三篇讲了集成学习（还有一篇集成学习的会在后面写），这篇我们来讲概率图模型！

我感觉概率图模型是机器学习里超难的一块（CMU 甚至有专门的一个系列课来讲它，非常的复杂…），这一篇我们来讲概率图模型中的一半——贝叶斯网络！（还有一半是马尔可夫网络，会在后面讲~

概率图模型简介

enen，在介绍贝叶斯网络之前，我们需要先对概率图模型有个大概的认识。

回顾这个系列之前所有的文章，到现在为止我们讲的所有模型（除了 HMM）都是针对两个变量之间的关系进行建模——输入 $x$，输出它对应的类别 $y$ 或值 $y$.

但是，现实的情况往往没有这么简单。现实中很可能出现很多变量相互依赖的情况，有些时候还会出现多个变量的依赖关系随着时间变化的情况，这意味着我们需要对这种复杂的依赖关系进行建模，而这就不是前面讲过的模型能够解决的问题了。

好在，有一种数据结构可以帮助我们描述并解决这种复杂的问题——图。（woq 想起了被图论支配的恐惧（bushi） 图的每个节点都可以看作一个变量，而图的边则代表这些变量之间的依赖关系。 同时，后面你会看到，图结构可以在很大程度上简化概率的计算。

概率图模型的核心思想就是，通过图结构建模变量之间的依赖关系，再利用图结构简化概率计算。

从这个核心思想出发，我们会得到两个问题：

1. 图结构是如何建模依赖关系的？（建模的是什么样的依赖关系？
2. 图结构是如何简化概率计算的？

对于这两个问题的不同回答，恰恰就得到了概率图模型的两个分支——贝叶斯网络（Bayesian Network）和马尔可夫网络（Markov Network）。

好吧好吧，先剧透一下。贝叶斯网络使用有向无环图建模变量之间的因果关系，通过 d-separation 简化概率计算；马尔可夫网络使用无向图建模变量之间的对称依赖关系，通过马尔可夫性简化概率计算。

在这篇文章中，我们主要探讨贝叶斯网络。

有向无环图（DAG）

em，为了更好地理解贝叶斯网络，我们先来复习一下有向无环图。

有向无环图，英文全称 directed acyclic graph，简称 DAG。

先放一个有向无环图的例子在这：

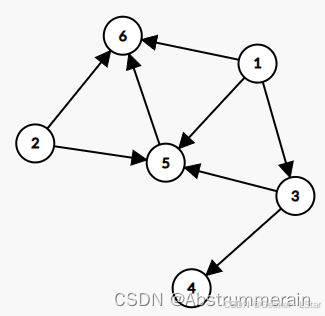
有向无环图，顾名思义，有两个主要的性质——有向性和无环性。

有向性是指，图中的每一条边都是有方向的。或者说，都是从一个节点出发，指向另一个节点的。
无环性是指，从一个节点出发，沿着箭头方向无论怎么走，都不会回到自身。

同时，我们还需要关注 DAG 中父节点和子节点的概念。
在 DAG 中，箭头发出的节点是父节点，箭头指向的节点是子节点。比如，在上图中，2、3、1 都是 5 的父节点，6 是 5 的子节点。（不是，但是我怎么感觉这个图描述的关系…emmmmm()()()()() 不是我啥也没说。

这些内容本身很好理解，重要的是它们在贝叶斯网络中的使用。我们后面会说到。

嗯！接下来让我们进入正题吧！

贝叶斯网络概述

okiiiii，我们来说说贝叶斯网络！

贝叶斯网络，英文全称 Bayesian Network，简称 BN。它使用有向无环图建模变量之间的因果依赖关系。具体来说，DAG 中的父节点代表 “因”，而子节点代表 “果”。举个例子，A 是 B 的父节点，说明 A 和 B 之间的关系是 “A 导致 B”，B 又是 C 的父节点，说明 B 和 C 之间的关系是 “B 导致 C”。当然如果你深思，这其中还有不少值得探讨的情况，我们在后面会一一说明。

比如，下图就是一个贝叶斯网络：

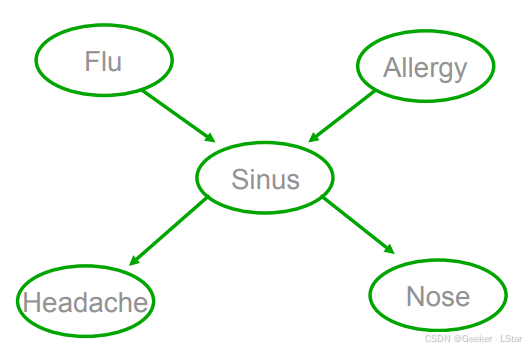
在这个图中，F 和 A 是 S 的父节点，说明 F 和 A 都有可能导致 A；H 和 N 是 A 的子节点，说明 A 有可能导致 H 和 N。贝叶斯网络中的因果关系就是通过 DAG 的有向边来建模的。

嗯，现在我们解释了在 “概率图模型简介” 中提出的第一个关键点——图结构（在贝叶斯网络中是 DAG）是如何建模变量之间的依赖关系的。现在我们转向第二个问题——图结构（DAG）是如何简化概率计算的。

我们先来看简化前的概率计算方式，即使用联合概率的链式展开。

$$P(F,A,S,H,N)=P(F)\cdot P(A|F)\cdot P(S|A,F)\cdot P(H|S,A,F)\cdot P(N|H,S,A,F)$$

也就是说，每个节点都依赖于它前面的所有节点。

推广一下，如果我们有 $n$ 个节点，那么联合概率分布就是：
$$P\left(X_1,X_2,\dots ,X_n\right)=P\left(X_1\right)\cdot P\left(X_2\mid X_1\right)\cdot P\left(X_3\mid X_1,X_2\right)\cdots P\left(X_n\mid X_1,X_2,\dots ,X_{n-1}\right)$$

可以看到，如果 $n$ 很大，这种计算方法简直就是…折磨 GPU 啊！难道就没有简单一点的方法了吗？

well，既然都问了这个问题，说明肯定时可以的（哈哈哈哈哈）。但是，具体要怎么简化呢，这还得从图结构的实际意义出发。
上面这种非人类的计算方式其实隐含了一个意思——我们要计算的节点（的条件概率），和除了它以外的每个节点相关。也就是说，所有的节点都会对这个节点的状态产生影响。

但是，真的是这样吗？

——No!

这就要说到贝叶斯网络中的条件独立性假设了，注意，这点非常重要。
贝叶斯网络的条件独立性假设是说，在给定父节点的情况下，子节点的条件概率只和父节点相关，而和其它非后代节点无关。
换言之，在给定父节点的条件下，子节点和所有非后代节点条件独立。

那么，我们就可以把上面那个极其难算的式子简化成下面这样：
$$P\left(X_1,X_2,\dots ,X_n\right)=\prod _{i=1}^{n}P\left(X_i\mid \mathrm{Pa}\left(X_i\right)\right)$$

其中 $Pa(X_i)$ 是 $X_i$ 的父节点。

当然，这背后的原理可没有这么简单，一切还要从 D 分隔说起咯…

D 分隔

D 分隔，或者说 D separation，是判断 DAG 中条件独立性的的方法。它是贝叶斯网络中至关重要（但同时又很不好理解）的一部分，可以说如果没有它，贝叶斯网络的条件独立性也就无从得出，整个后续的计算也就没法进行了。

D 分隔有三种基本类型，从这三种类型出发，我们可以组合得到更多复杂的 DAG；反过来，无论多么复杂的 DAG，在判断两个（或两组）节点在给定另外一些（或一些组）节点时的条件独立性的时候，我们都可以使用 D 分隔来做，后面会说到详细的规则。

不过，在我们深入讨论 D 分隔的三种类型及其对应的条件独立性之前，我们需要先搞明白——条件独立性是什么意思？？

条件独立性

首先我们来复习一下，独立性是什么意思来着？两个变量是独立的，可以通过什么样的数学公式来表达？

我记得在朴素贝叶斯那篇中我说过，如果两个变量是独立的，那么它们的联合概率等于它们自身概率的乘积，即：
$$P(A,B)=P(A)P(B)$$

对于多个变量也是类似的。

这里的独立性，也可以叫做边缘（marginal）独立性，可以类比边缘概率来理解。即在没有任何额外信息的条件下，两个变量的独立性。

那么，和概率类似，如果有额外信息呢？具体来说，如果我们给定一些其它变量呢？

这就到了条件独立性上场的时候了。

条件独立的定义是：如果在给定第三个变量的条件下，两个变量的条件联合概率等于它们各自条件概率的乘积，就称这两个变量是条件独立的。公式如下：
$$P(A,B|C)=P(A|C)P(B|C)$$

上面的公式等价于：
$$P(A|C)=P(A|B,C)$$

也就是说，A 和 B 原本不是独立的，但是给定 C 后，A 和 B 就独立了。这样的独立就称作条件独立。（注意理解条件独立和边缘独立的区别o~

再通俗一点，C 解释了 A 和 B 之间的所有关系（相关性），在给定 C 后，任何其它的变量都不会对 A、B 之间的关系做出更多的解释。所以在 C 给定后，A、B 条件独立。

注意，A、B、C 不只可以代表单个变量，也可以代表一组变量。

豪德！我想条件独立性这个概念现在应该已经阐述的比较清楚了。接下来我们可以来考虑考虑 D 分隔的三种情况了…

well，在开始后续的内容之前，我们需要首先明确一下依赖关系中的 head 和 tail：head 代表父节点，或者说发出箭头的节点；tail 代表子节点，或者说箭头指向的节点。

那我们来具体看看 D 分隔的三种类型吧!

tail-to-tail 类型（Fork）

首先是第一种类型，tail-to-tail，也叫共父类型。如下图所示。

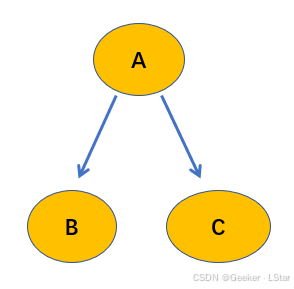
在这种类型中，当 $A$（父节点）被观测到时，$B$ 和 $C$（子节点）之间是条件独立的。
写成数学语言就是：
$$P(B,C|A)=P(B|A)P(C|A)$$

同时，如果 A 没有被观测到，则 B、C 之间的条件独立性不成立。

no why，这是规定（（（

这个类型告诉我们，当父节点给定的时候，子节点和它的兄弟节点条件独立。

head-to-tail 类型（Chain）

第二种类型是 head-to-tail 类型，也叫链式类型，如下图：

当然，方向也可以反过来，变成 C$\to$B$\to$A，不影响。

在这种类型中，当 $B$（父节点）被观测到时，$A$（祖先节点）和 $C$（子节点）之间是条件独立。数学表达式为：
$$P(A,C|B)=P(A|B)P(C|B)$$

同样的，如果 B 没有被观测到，那么 A、C 之间的条件独立性不成立。

这个类型告诉我们，当父节点给定的时候，子节点和它祖先节点条件独立。

head-to-head 类型（Collider）

head to head，这是第三种类型，也叫对撞类型，V 型类型等等，有很多名字。。（这也是为什么我使用 head 和 tail 来描述，这是最通用的说法，中文世界中的名字太多了，，，）

注意，和前两种类型相比，head-to-head 有点 tricky，如下图所示：

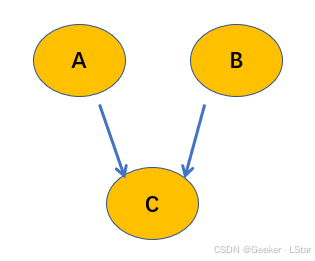
前面我们都在说父节点被观测到的情况，但在这种类型中，情况稍稍发生了一些变化…

在 h-to-h 类型中，当 $C$（子节点）被观测到的时候，$A$ 和 $B$（父节点）非条件独立。公式为：
$$P(A,B|C)\ne P(A|C)P(B|C)$$

而大概 $C$ 没有被观测到时候，$A$ 和 $B$ 独立（注意这里是独立而非条件独立），即：
$$P(A,B)=P(A)P(B)$$

一定要注意呀，这个类型和前面的都不一样，首先它被观测到的是子节点，第二它的结论是非条件独立，恰好和上面两种类型反过来。

这个类型告诉我们，当子节点给定的时候，它的父节点们非条件独立。

以上就是 D 分隔的三种基本情况，了解了这三种情况后，我们就可以从它们出发，推导更复杂的网络中的条件独立性。

嗯…如果你觉得上面这些东西实在是太复杂了，搞不懂，你可以忽略它们，直接记住下面要讲到的结论就可以，这些内容是为了推导出下面的结论做铺垫的。

ennnn!! 以上就是 D 分隔的三种类型，现在我们可以从它们出发，开始推导贝叶斯网络的条件独立性了…!!! 这是整个贝叶斯网络中最核心的部分！

启动！

贝叶斯网络的条件独立性

来了来了！终于来了！这是贝叶斯网络的核心！它很短，但很重要！
（这也是为什么我单独给它开了一个部分哈哈哈哈（（

贝叶斯网络的条件独立性是指，在给定父节点的情况下，子节点和所有非后代节点条件独立。

天知道我用了多长时间才彻底理解它！。。。。

在这一部分，我们的目标就是，从 D 分隔出发，一步步说明贝叶斯网络条件独立性的合理性。

换言之，在这一部分，我们希望搞明白，为什么贝叶斯网络的条件独立性是这样的。

没错，它可不是随便规定的（不像朴素贝叶斯中的独立性假设），它是可以从 D 分隔中严格推导出来的。

在开始之前，请牢记 D 分隔的三条规则：
1）当父节点被观测到时，它的子节点之间彼此条件独立
2）当父节点被观测到时，它的子节点和祖先节点条件独立
3）当子节点被观测到时，它的父节点之间彼此非条件独立

从这三条规则出发，我们来分析一种情况，如下图所示。

（当然，除此之外，还有很多很多复杂的情况，不过我们的重点是从 D 分隔出发，推导出贝叶斯网络的条件独立性，而不是单纯的 D 分隔练习，所以更复杂的情况在此处就不展开讨论了。

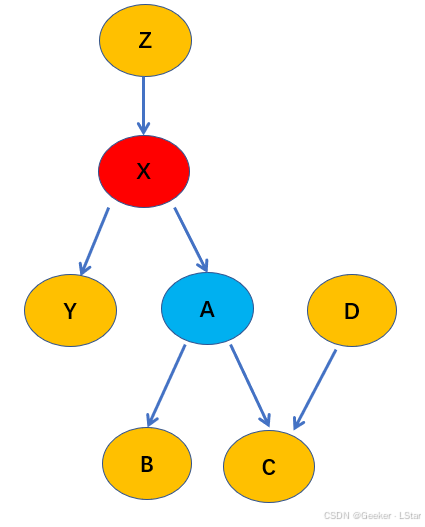
现在，节点 X 被观测到了（红色），请问节点 A（蓝色）的条件独立性？

首先，根据三条规则的第一条（tail-to-tail），A 它的兄弟节点，或者说 X 的其它子节点，在这个例子中也就是 Y，条件独立。

then，根据三条规则的第二条，A 和它的祖先节点，在这个例子中也就是 $Z$，条件独立。

好的，接下来，我们重点考虑 A 和它的子节点 B、C，以及它的子节点的其它父节点 D，之间的条件独立性。

首先我们先不考虑子节点 B、C，只考虑 A 和 D 的条件独立性。

根据三条规则的第三条，当 C 没有被观测到的时候，A 和 D 是独立的，同时 X 不和 A、D 形成 head-to-head 结构，这表明在给定 X 且不给定 C 的条件下，A 和 D 关于 X 条件独立。

第二步，我们把 B、C 也纳入考虑。

根据三条规则的第三条，此时 A$\to$C$\leftarrow$D 形成 head-to-head 结构，且 C 被观测到，所以此时 A 和 D 条件不独立。这表明，原本条件独立的两个节点（A 和 D），可能会在给定 A 的后代节点（C）之后，变得非条件独立。
也就是说，后代节点会引入额外的相关性。

同时，因为 A 和 B、C 之间本来就直接相连，根据 D 分隔的三条规则，它们之间显然条件不独立。

趁热打铁，更进一步思考。
对于一个节点来讲，和它有关系的节点有哪些种类？只有以下五种：

1. 父节点
2. 兄弟节点
3. 祖先节点
4. 后代节点
5. 后代节点的其它父节点

现在，我们已经根据 D 分隔，说明了在给定父节点的情况下，子节点（给定的父节点的子节点）和它的兄弟节点、祖先节点、后代节点的其它父节点，都是条件独立的；同时，它和它的后代节点是非条件独立的。

把这句话浓缩一下！
在给定父节点的情况下，子节点和所有非后代节点条件独立。
这是什么！这不就是贝叶斯网络的条件独立性吗！

这里再说明一下为什么是和 “所有非后代节点条件独立”，这句话其实有两层意思。
第一层，给定父节点时，子节点和它的后代节点非条件独立。
第二层，给定父节点时且不给定后代节点的时候，子节点和所有其它节点（也就是所有非后代节点）条件独立；但是，一旦引入后代节点，子节点就不一定和所有非后代节点条件独立了，因为后代节点会引入额外的相关性（比如我们上面说到的 head-to-head 的例子）。

好耶！！~（撒花!!

那么，现在我们可算是真正明白了贝叶斯网络中的条件独立性了！

贝叶斯网络的参数学习

okay，现在我们终于明白贝叶斯网络的条件独立性是怎么一回事了！接下来，我们可以使用它来做更多的事情…

前面说过，对于贝叶斯网络，我们需要确定的是它的结构和参数。按理说应该是先确定结构，再根据确定的结构去 “寻找” 参数。不过，实际情况和这个乍一看很正确的想法稍有出入，后面我会说到，这里先卖个关子啦~

我们先来讲贝叶斯网络的参数学习（而不是结构学习），后面你会知道这个顺序的道理。

em，在一切开始之前，我们需要先明确，在贝叶斯网络中，我们要学习的 “参数” 是什么？

这涉及到一个新的概念——条件概率表（conditional probability table，简称 CPT）。这个表给出了每个节点的条件概率，即在这个节点的父节点取不同值的时候，这个节点出现（为真）的概率，如下图。

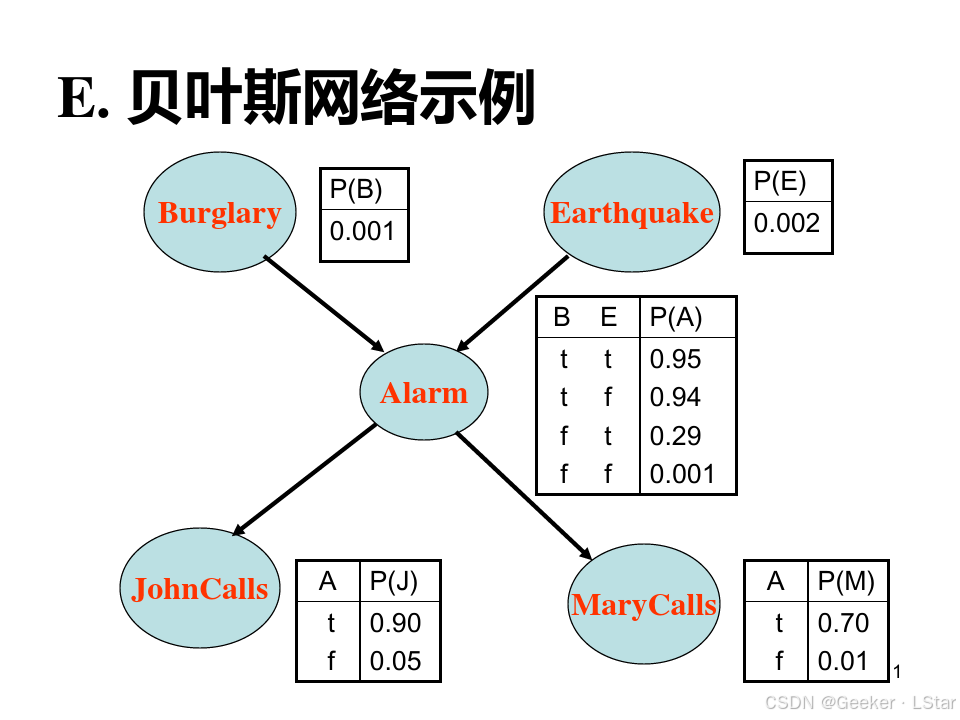
在这个图中，节点 A 的条件概率表表示的是，在父节点 B 和 F 取不同的值（tt/tf/ft/ff）的时候，A 发生的概率。节点 J 和 M 的 CPT 也是一个意思。

显然，CPT 是建立在条件独立性假设上的。

我们要学习的就是 CPT 中 $P$ 列的值。即在父节点取特定值的时候，子节点取特定值（在上面的例子中就是为真）的概率。

注意，如果一个节点没有任何的父节点，那么我们学习的就是它的边缘概率，比如上图中的 B 和 E。

豪德（）现在我们可以正式开始估计这些参数了。

完全数据：极大似然估计

嗷aooooo，经过前面那么多篇文章的洗礼，我想你对参数学习应该已经相当清楚了。

对于完全数据，也就是不含隐变量的数据，我们可以直接通过极大似然估计学习参数；而对于不完全数据，也就是含有隐变量的数据，我们需要通过 EM 算法，迭代式地求解参数。

如果你对极大似然估计（MLE）或 EM 算法还不了解，可以参考我之前的一些文章：

【初中生讲机器学习】12. 似然函数和极大似然估计：原理、应用与代码实现

【初中生讲机器学习】15. EM 算法一万字详解！一起来学！

我们先来看完全数据的情况，也就是使用极大似然估计的情况。

还是用上面那个例子：

按照极大似然估计的思想，我们的目的是什么呢，是找到让已有数据的出现概率最大的参数 $\theta$，即：
$$\theta =\underset{\theta }{\mathrm{argmin}}P(D|\theta )$$

其中 $D$ 代表所有数据，共有 $K$ 组，即 $D=\{(f_1,a_1,s_1,h_1,n_1),(f_2,a_2,s_2,h_2,n_2),...,(f_K,a_K,s_K,h_K,n_K)\}$

我们把这个式子展开，得到：
$$P(D|\theta )=\prod _{k=1}^{K}P\left(f_k,a_k,s_k,h_k,n_k\right)$$

根据条件独立性假设，我们可以简化这个式子：
$$P(D|\theta )=\prod _{k=1}^{K}P\left(f_k\right)P\left(a_k\right)P\left(s_k|f_k{a}_k\right)P\left(h_k|s_k\right)P\left(n_k|s_k\right)$$

嗯，接下来把连乘变成连加：
$$\log P(D|\theta )=\sum _{k=1}^K\log P\left(f_k\right)+\log P\left(a_k\right)+\log P\left(s_k|f_k{a}_k\right)+\log P\left(h_k|s_k\right)+\log P\left(n_k|s_k\right)$$

豪德，现在比如我们要求当 $F=i,A=j$ 的时候，$S$ 出现（即 $S=1$）的概率（回忆一下 CPT），我们只需要让极大似然函数对对应参数的偏导数为 0 就可以了，即：
我们要求：
$${\theta }_{s=1|ij}\equiv P(S=1|F=i,A=j)$$

求解式子为：
$$\frac{\partial \log P(D|\theta )}{\partial {\theta }_{s=1|ij}}=\sum _{k=1}^K\frac{\partial \log P\left(s_k|f_k{a}_k\right)}{\partial {\theta }_{s=1|ij}}$$

解得：

$${\theta }_{s=1\mid ij}=\frac{{\sum }_{k=1}^K\delta \left(f_k=i,a_k=j,s_k=1\right)}{{\sum }_{k=1}^K\delta \left(f_k=i,a_k=j\right)}$$

其中 $\delta$ 是特征函数——在后面的特征成立的时候，函数取值为 1，否则取值为 0.

em，如果你对上述求解步骤中的任何一步有疑惑，不妨去看看极大似然估计那篇文章，那篇文章对每个步骤的原理都做了详细的解释。

嘿嘿，不难发现，条件独立性假设极大地简化了参数求解。

按照这套路子，我们可以求解出 CPT 中的任何一个条件概率。比如，我们把上面的式子进一步特殊化，得到：
$${\theta }_{s=1|i=1,j=0}=P(S=1|F=1,A=0)$$

解得：
$${\theta }_{s=1\mid i=1,j=0}=\frac{{\sum }_{k=1}^K\delta \left(f_k=1,a_k=0,s_k=1\right)}{{\sum }_{k=1}^K\delta \left(f_k=1,a_k=0\right)}$$

这个式子表示的就是，当两个父节点 $F$ 和 $A$ 的取值分别为 1 和 0 的时候，子节点 $S$ 取值为 1 的概率。

至此，我们已经完整地梳理了在完全数据的情况下，贝叶斯网络的参数学习方法。
其实就是普通的极大似然估计啦，只是 $P(D|\theta )$ 会长一点，某些子节点依赖的父节点会多一些。但实际上整个思想是一样的。

en!! 接下来我们来看看，当数据中有隐变量的时候，又应该如何求解。

不完全数据：EM

呃呃呃（）其实这部分也很简单。上一部分是直接套极大似然估计，这一部分是直接套 EM。

还是上面那个例子（绿色的图），但是，现在 $S$ 无法被观测。
换言之，现在我们只能观测到 $F、A、H、N$，而没有办法观测到 $S$.

So，极大似然估计行不通了，我们需要用 EM 算法。

我们把所有可观测数据记作 $X$，把所有不可观测数据（隐变量）记作 $Z$.

按照 EM 算法的思想，我们首先通过上一轮迭代求出的参数估计隐藏变量 Z 的分布，然后利用估计得到的 Z 和已知的 X，求解这一轮的参数。EM 算法最终可以简化为最大化 Q 函数的问题，如下。
$$Q(\theta ,\overline{\theta })=\sum _{Z}P(X,Z|\overline{\theta })\log P(X,Z|\theta )$$

其中 $\theta$ 是上次迭代求出的参数（CPT 表中的值），$\theta$ 是本次迭代待求的参数，$X$ 是所有的观测数据，$Z$ 是所有的隐变量。

嗯，至于这个 Q 函数是怎么来的，在 EM 算法那篇我们已经给出了详细的推导过程，在这里就不再重复推导了（EM 的推导过程简直太长了!!），直接使用结论。你可以在那篇文章中找到详细的推导过程。

至此，不完全数据构成的贝叶斯网络的参数学习也搞定啦！！我们可以进入到下一个 part——贝叶斯网络的结构学习。

贝叶斯网络的结构学习

还记得在参数学习部分最开始的时候，我们遗留的一个问题吗？——为什么先讲参数学习，再讲结构学习？

等看完这个 part 你就明白了，嘻嘻。

结构学习，顾名思义，学习贝叶斯网络的结构，也就是各个节点之间的依赖关系。

贝叶斯网络是有向图，所以依赖关系在这里有两层含义：

• 哪两个节点之间有边相连？
• 对于两个相连的节点，谁是父节点，谁是子节点？

你可能会想，呃，，，这么复杂，那我岂不是要把所有可能的依赖情况，从所有节点彼此独立（注意是独立而非条件独立），到所有节点两两之间都有边相连，全都考虑（暴力）一遍？？而且还得考虑边的方向问题，这得花多少时间和计算资源啊…

weeeeell 显然，这种纯暴力的方法无论如何是行不通的。我们需要一些更为 heuristic 的方法…

接下来要讲的两种方法就是这样的!!

评分方法

首先是评分方法。

字面意思，它很好理解：每个结构都会有一个对应的评分，我们选择评分最高的结构。

那么，有两个关键问题：

• 怎么寻找结构？（前面说了，显然暴力是行不通的。。
• 使用什么样的评分准则（函数）？

well，要不在这里先给出答案吧。

对于第一个问题，评分方法使用贪心策略，一步一步迭代解决。
具体来说，我们会从一个全空（或全满）的图出发，在每一步（每一次迭代）都尝试以下三种操作。

1）增加一条边
2）删除一条已有边
3）调换一条已有边的顺序（父子节点互换）

通过这三种操作，我们可以得到很多的新网络结构。对于每种新网络结构，我们都计算它们的评分（具体评分函数是什么后面会说到）。然后，我们选出评分最高的网络结构，作为这一次迭代得到的新网络结构。

比如，我们现在有个完全空的图：

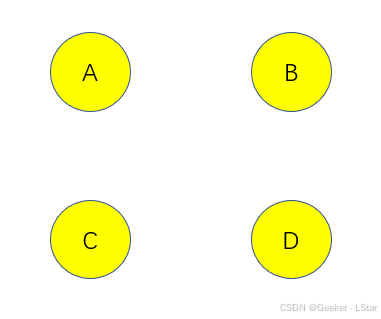
在第一步中，我们可以尝试在 AB 中添加边（A 指向 B 或 B 指向 A）、在 BC 中添加边（同上），等等。对于每一个添加边后得到的新网络，我们都计算它在评分函数上的得分，并选择评分最高的网络作为这一轮得到的网络。

比如说，添加 A 指向 B 的边，新网络的得分为 $S_1$；添加 B 指向 C 的边，新网络的得分为 $S_2$，…，如果在所有这些得分中，$S_1$ 最大，那么在这一步，我们就添加由 A 指向 B 的边，即：

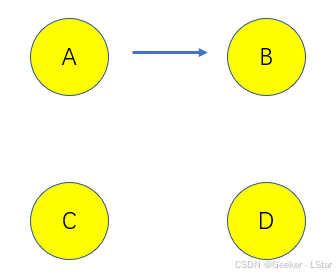
这就是我们在第一次迭代（贪心）后得到的网络结构。

嗯，可以看到，在选择网络结构的时候，我们选择的是 “评分最高的结构”，但到现在为止，我们好像还没有说明这个评分具体是怎么做的。
（这是最开始说的第二个问题。

sooooo 让我们来看看第二个问题…

对于这个问题，通常有两种处理方法——可以直接使用似然函数（或 EM 函数，针对含有隐变量的问题）作为评分函数，也可以加入控制模型复杂度的项，使用贝叶斯信息准则（BIC 准则）作为评分函数。通常而言，为了避免模型过拟合，我们会使用 BIC 准则作为评分函数（类似于正则化项）。

但是注意，虽然贪心策略极大地降低了计算复杂度，但它经常会陷入局部最优解。换言之，贪心策略给出的网络结构不一定是最优的网络结构（或者说在大部分情况下，都不是最优的网络结构）。
在大多数情况下，精度和计算复杂度是无法兼得的。

如果使用极大似然估计，则最终式子如下，和我们在前面讲条件独立性的时候用到的式子一样：
$$L(G)=\prod _{i=1}^{n}P(X_i|\text{Parents}(X_i),\theta )$$

其中 $G$ 代表图结构，下同。
我们选择使得这个式子（似然函数）最大的结构作为这一轮迭代的结构。

使用 EM 也是类似的道理，也和我们在参数学习中说到的式子是一样，即：
$$Q(\theta ,\overline{\theta })=\sum _{Z}P(X,Z|\overline{\theta })\log P(X,Z|\theta )$$

其中 $X$ 是观测变量，$Z$ 是隐变量。

然后我们来说说 BIC 信息准则。
在实际情况中，如果只使用似然函数或 EM 函数作为评分函数，模型大概率会过拟合。因为模型为了提高评分，会倾向于学习更多的依赖，把很多实际上没有关系的节点也连起来。这会导致对数据的过度解释。

这可不是我们想看到的。

so，我们需要在评分函数中加入一个专门评判模型复杂度的项，这个项会和似然函数项互相制衡。如果模型想在整个评分函数（而不是仅仅在似然函数上）取得最大值，就必须不能让这个项太大，也就是说，必须得控制结构的复杂性。

BIC 的公式如下：
$$\text{BIC}(G)=-2\log L(G)+k\log (n)$$

其中，$L(G)$ 是似然函数项，$n$ 代表模型的参数数量，系数 $k$ 用于调整前后两部分的重要程度（$k$ 大，说明更看重结构的复杂程度，$k$ 小，说明更看重似然函数值，也就是对数据的拟合程度）。在实际任务中，$k$ 可以通过交叉验证得到。

我们的目标就是找到使得 BIC 最小的模型结构。

另外，有必要说明一下 BIC 和正则化的区别（我发现前面我一直在说它们很相似，但其实它们之间也有显著的不同）。

BIC 常用在模型（结构）选择，我们对比不同模型结构的 BIC，选出 BIC 值最大的结构；而正则化常用在模型训练的过程中，

简言之，BIC 用于多个模型的对比和选择，而正则化用在一个模型训练的过程中，控制模型的复杂度。

ok，简单总结，评分方法使用贪心算法寻找网络结构，并从似然函数值（拟合程度）和网络复杂度两个方面对网络结构进行评估。

现在可以解释我在前面卖的关子了（嘻嘻）。之所以先讲参数学习而非结构学习，是因为在结构学习的过程中，对于每种结构，我们都需要先学习出它的参数，再根据参数对应的似然函数值和复杂度计算出评分函数。相当于，在进行结构学习的时候，已经包含了参数学习。

换言之，对于一个未知结构的网络，结构学习和参数学习是交替进行的。对于任何一个可能的结构，我们都需要学习它的参数，根据参数计算它的评分，选择评分最高的结构，再在这个新结构的基础上进行下一轮迭代…

en!! 以上就是评分方法的基本思想和的计算流程，可以看到其实没有太多数学公式，还是比较友好的，嘿嘿。

除了评分方法，还有一种方法——约束方法，也经常用于贝叶斯网络的结构学习。

我们接下来来看看约束方法吧！

约束方法

约束方法，这个名字就不像评分方法那么好理解了。约束，约束的是什么？

well，还是开门见山。在这里，约束是指对条件独立性的约束。

约束方法有很多，其中最有代表性的是 PC 算法（Peter-Clark 算法）。

先大致概括一下 PC 算法的流程。
PC 算法从一个完全图（即每两个节点之间都有边相连的无向图）开始，利用数学上判断条件独立性的方法，比如卡方检验、fisher 精确检验等，判断两个变量是否（条件）独立。对于那些条件独立的变量，移除它们之间的边。当没有边可以移除的时候，我们就得到了最终的图结构。

啊啊啊好吧，这么一大坨好像并不是很清晰…我们还是一步步来看吧。

首先，我们从一个完全图，即图中每个节点之间都有边的无向图开始。如下左图所示。
（注意开始的时候是无向图o，具体怎么把无向图变成有向图后面会说~

我们设定一个条件集合 $S$，最开始 $S$ 为空，$S$ 是干什么的你很快就会知道。

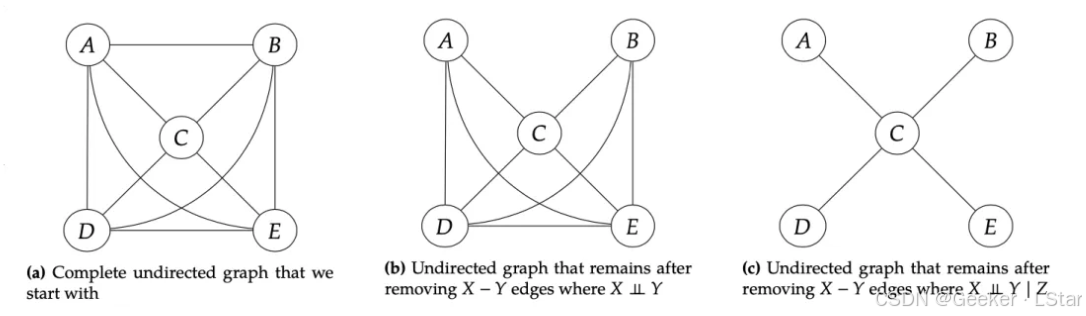
well，下面进行第一步——独立性检验。

在这一步，我们不给定任何变量，而是单纯判断这些节点两两之间的独立性，对于那些彼此独立的节点，我们移除它们之间的边。这个过程对应于上中图。

嗯，现在，那些本身就独立的变量之间的连接被去除了，我们得到了新的图结构，它相比于完全图应该已经有了很大程度的简化。

现在，我们在 $S$ 中添加一个变量，比如 $Z$。

然后，对于图中剩下的所有有边相连的节点，我们都判断它们在给定 $Z$ 的情况下是否是条件独立的。如果条件独立，则移除它们之间的边。这个过程对应于上右图。

接下来，我们再向 $S$ 中添加一个变量，比如 $W$。

同样的，对于图中所有有边相连的节点，我们都判断它们在给定 $Z$ 和 $W$ 的情况下是否是条件独立的。如果条件独立，则移除它们之间的边。

就这么以此类推下去，直到没有任何的边可以删除，或 $S$ 中的元素个数达到最大。

嗯，这就是约束方法的大致流程，你可能发现，诶好像并没有说明具体怎么判断独立性或条件独立性诶？？？

weeeeeell，这涉及到卡方检验和条件卡方检验，由于内容很多（而且包含很多的数学，，），所以我会单独开一篇文章来讲，又开新坑了啊哈哈哈哈哈（转圈圈（（

ennn，约束方法其实并不复杂，概括一下就是不断扩大条件集，判断在当前条件集的情况下图中变量的条件独立情况。 对于那些在给定条件集后条件独立的变量，我们删除它们之间的边。

豪德，下面我们进入下一个话题——到目前为止，PC 算法处理的一直是无向图，但是，在贝叶斯网络中，我们最终需要得到一个有向图——这怎么办呀？

well，为了更好地回答这个问题，我们需要先复习一下 D 分隔的三种情况。

还是按照我们之前的顺序，下图从左到右依次是第 1-3 种情况。

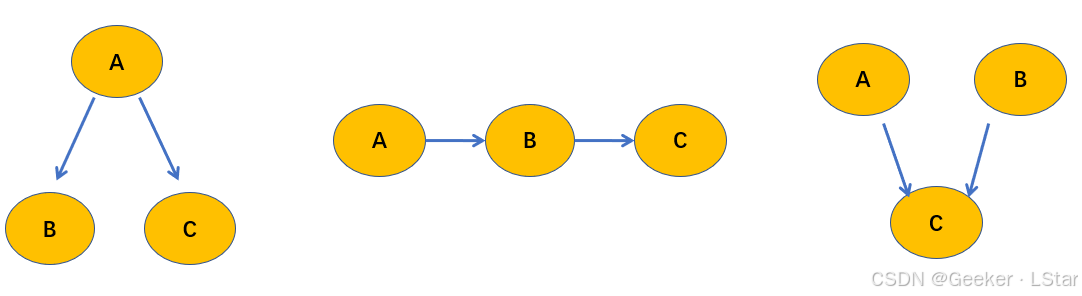
对于第一种情况，给定 A（中间节点）的时候，B 和 C 条件独立；不给定 A 的时候，B 和 C 非条件独立。

对于第二种情况，给定 B（中间节点）的时候，A 和 C 条件独立；不给定 B 的时候，A 和 C 非条件独立。

对于第三种情况，给定 C（中间节点）的时候，A 和 B 非条件独立；不给定 C 的时候，A 和 B 条件独立。

诶你发现了什么，第一种情况和第二种情况的叙述完全一样诶，，，这说明，我们没有办法区分第一种和第二种情况，我们唯一能够判定的就是第三种情况。

所以，对于使用约束方法后剩下的所有边，我们都判断它们是否属于第三种情况，这可以帮我们确定一些边的方向。

具体来讲，如果在给定一个节点的情况下，其它两个和它直接相连节点的非条件独立；但在不给定这个节点的情况下，其它两个和它相连的节点条件独立，那么，其它两个节点就是这个节点的父节点，即 D 分隔三种情况中的 head-to-head.

那么，对于其它不确定方向的边，怎么办？

eerrr 这就只能继续用类似于评分方法的启发式方法啦（）具体做法和评分方法非常类似，这里不再赘述。

好耶，讲完约束方法（PC 算法），我们把它和评分方法做一个小小的对比。

评分方法完全基于启发式方法来选择结构，（虽然比暴力遍历所有结构要好一些，但）它需要搜索大量可能的结构，并对每一个结构都计算评分，这导致它比较耗时。不过它学习出的网络通常性能较好，虽然这个结构可能在一定程度上缺乏数学解释性。

约束方法和评分方法几乎相反，它使用严格的数学方法来选择结构，这保证了它学习出的结果的可解释性，但这同时导致了它对数据数量和数据质量有着更高的要求（或者说更为敏感），这导致它更难学习出 robust 的网络结构（因为基于独立性检验的方法很容易受到数据噪声的影响）。

嗯！！那上面就是贝叶斯网络结构学习的两种主要方法啦~

现在我们已经讲完了贝叶斯网络的参数学习和结构学习，但是你有没有发现，诶它好像有那么些局限性…？

动态贝叶斯网络

在前面的内容中，我们考虑了多个变量之间的依赖关系。但是，你有没有想过，有些时候这些依赖关系并不是一成不变的诶，它们完全可能随着时间的变化而变化。

对于这种情况，前面讲的（静态）贝叶斯网络就不能很好地处理了，因为它没有把时间考虑进去。

我们需要在原始贝叶斯网络的基础上，把时间维度引入进来。大概思路如下图所示，即，每个节点的状态（取值）不仅与这个时间步的其它节点有关，也和上一个时间步的一些节点有关。

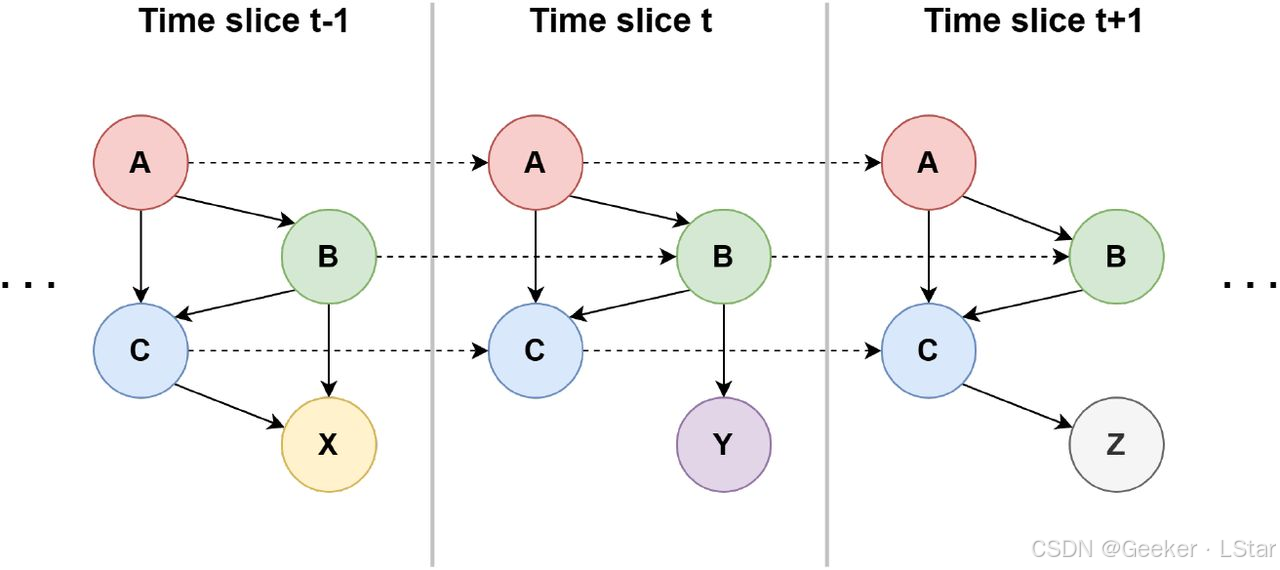
这种将时间纳入考虑的贝叶斯网络，就被称为动态贝叶斯网络，英文简称 DBN。

动态贝叶斯网络的参数学习和结构学习和贝叶斯网络是一样的，因为它其实只是多了一个依赖——后一个时间步的某变量对前一个时间步的一些（或一个）变量的依赖。在这里就不再展开单说了。

特例：隐马尔可夫模型

嗯！！隐马尔可夫模型（HMM）是动态贝叶斯网络的一个特例，它的结构如下所示：

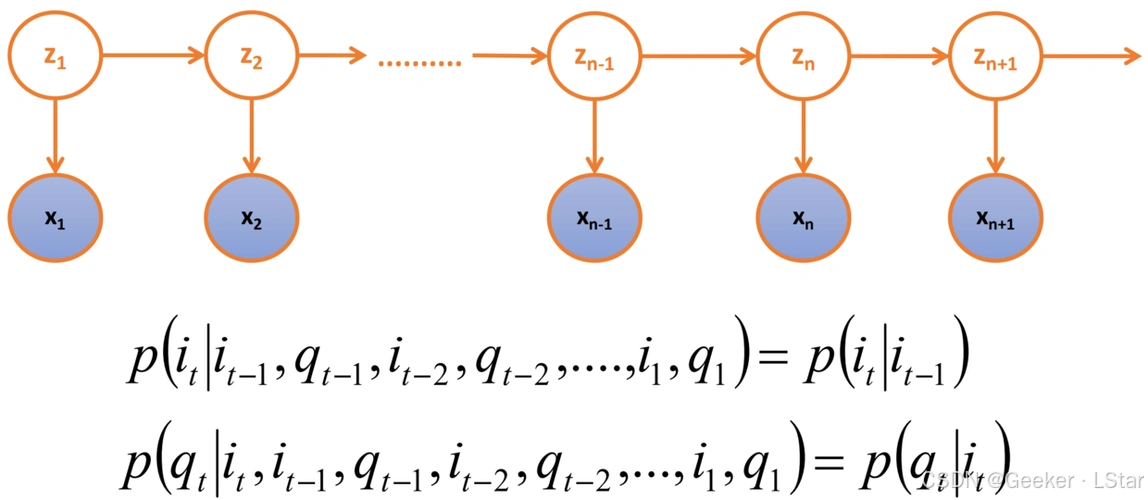
其中上层（Z）代表隐藏的状态序列，下层（X）代表观测序列。可以看到，每个时间步的隐藏状态都依赖于前一个时间步的隐藏状态，同时每个时间步的隐藏状态又会影响这个时间步的观测。HMM 是一个典型的动态贝叶斯网络。

ennmmm 不过，其实在写这篇之前，我就已经写过 HMM 的详细讲解啦，所以 HMM 的相关内容就不在这里展开了。下面是 HMM 详解的 link!：

【高中生讲机器学习】20. 隐马尔可夫模型好难？看过来！（上篇）

【高中生讲机器学习】21. 隐马尔可夫模型好难？看过来！（下篇）

可以进一步看一看 HMM！会让你对贝叶斯网络和动态贝叶斯网络都有更实例化的理解~

哇！！那我们这一篇的所有内容就讲完了耶！！

---

嘿嘿嘿，那这一篇就到这里啦~~我们下一篇再见！下一篇可能会讲概率图模型家族的另一大部分——马尔可夫模型！keep fooooollow!

这篇文章系统地贝叶斯网络，包括贝叶斯网络的条件独立性、参数学习和结构学习等，希望对你有所帮助！⭐
欢迎三连！！一起加油！🎇
——Geeker_LStar