1.1 欢迎来到机器学习

什么是机器学习？

搜索引擎对网页进行排名，自动识别人照片与名字对应， 视频网站对类似视频推荐，手机上的语音转文字功能，语音助手siri，识别垃圾邮件，帮助优化风力涡轮机发电，协助医生做出准确诊断，将计算机视觉引入工厂流水线缺陷检测。

1.2 机器学习的应用

学习最先进的算法和实践机器学习算法，人工智能的现状，重要的实用技巧以及提高算法性能的技巧。动手实现它们，看它们如何运行的。

最重要的机器学习算法：

我们可以编程实现如何找到从a到b的最短路径如GPS，但无法写出实现：执行网络搜索，理解人说话的意思的程序，疾病诊断的程序或制造一辆自动驾驶汽车。关键是如何让机器自己学会。

AGI Artificial General Intelligence 人工通用智能

途径也许是使用学习算法：learning algorithms

麦肯锡预计人工智能产业链达到13万亿美元在2023前

2.1 什么是机器学习

Arthur Samuel 在1959年定义为让计算机在没有明确编程的情况下学习的研究领域。

在1950年写出的一个跳棋程序击败了跳棋冠军，学习那些位置是好位置，那些位置是不利位置，通过大量的对局学习出的。因为计算机可以和自己下数以万计的对局，所以可以总结出大量的经验。

 better 不是为了让你一次性作对，而是让你实践所学知识。

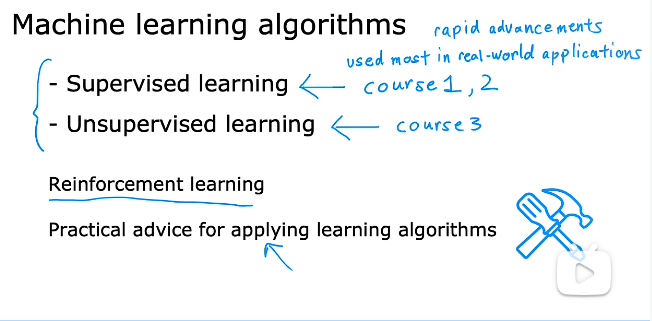
 机器学习算法分为：监督学习和非监督学习

监督学习算法：大多数用到是监督学习算法，也是发展最快的领域，course1和course2主讲监督学习算法。

非监督学习算法：course3主讲

强化学习算法：略有提及。

强烈建议亲自上手学习如何使用这些工具。

希望熟练使用这些工具，知道如何设计和制造严谨的机器学习系统。

2.2监督学习算法1--回归算法

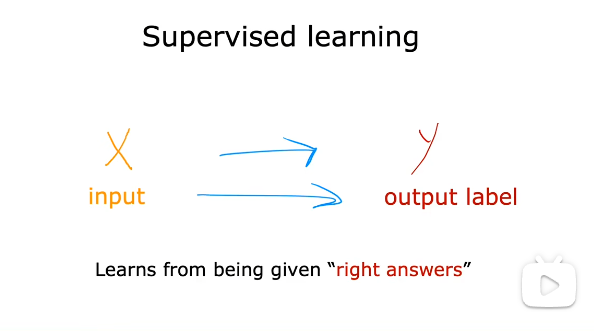
 从正确标签中学习

先给予一些学习数据，给予正确的标签，学习映射然后应用于新的数据中。

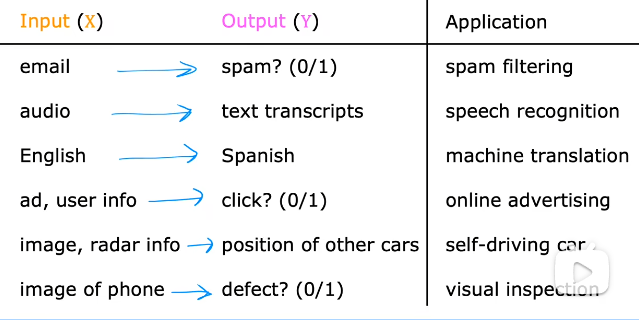
线性 回归：通过输入数据，输出连续值。

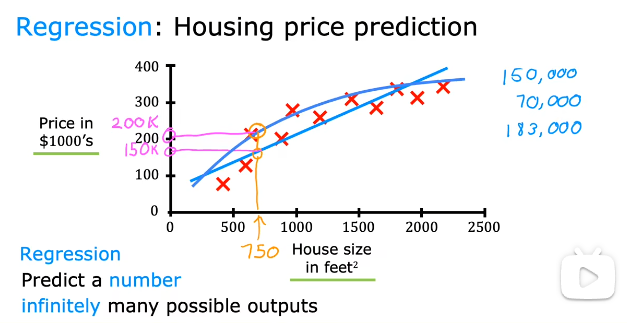
 对数据的拟合可能是线性的，也可能是曲线。

2.2监督学习算法2--分类算法

分类算法：乳腺癌检测。区别于回归的连续值，分类是预先规定好的离散值。

 

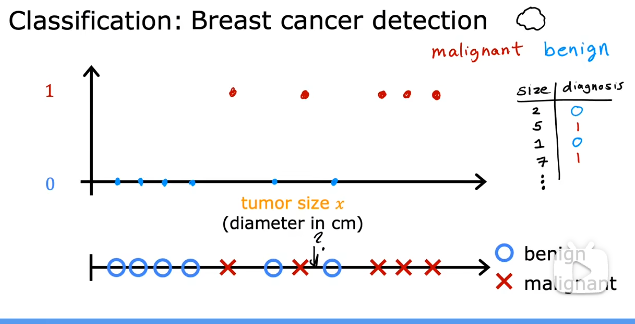
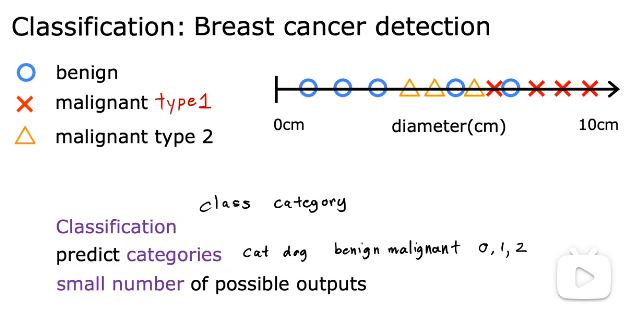
 预测类别可以是：猫狗、良性恶性、012

class和category是同义词

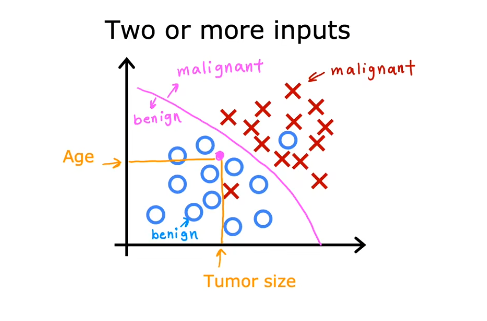
 输入特征数量可能是两个或更多，使用算法找到分界线。

 回归算法：预测值是实数。

分类算法：预测值是数字或者种类。

2.4 非监督学习算法1--聚类学习算法

非监督学习算法：让算法自己在无标签数据中寻找一些类似的结构或者有趣的数据.

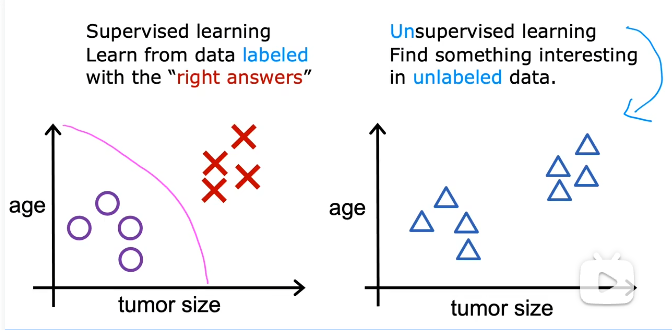
 聚类学习算法：将未被标记的数据放入不同的集群中。

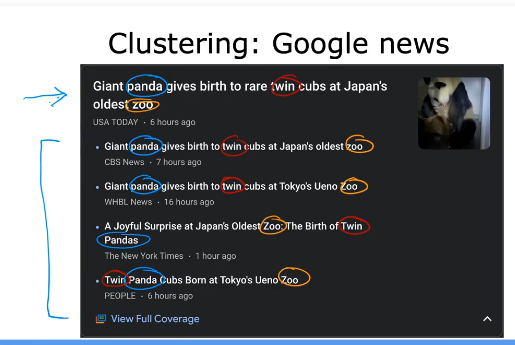
例如：谷歌news中：找到相似单词的文章，并把它们放在一个聚类中。由算法自动计算得出。

 例2：DNA数据聚类的无监督学习案例

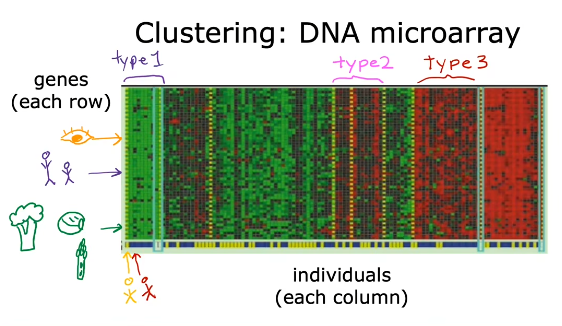
每一列代表一个个体，每一行代表一个基因，这个基因可能与视觉有关，与身高有关，与是否喜欢吃蔬菜有关，最后非监督学习算法将相似的分为一类，从图中颜色可以看出。 

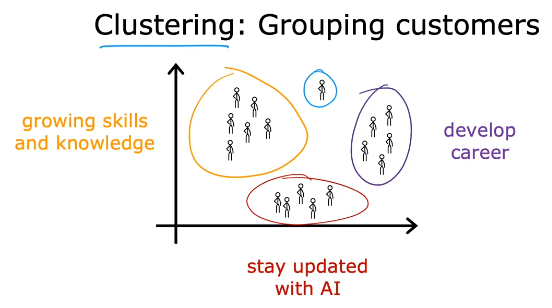
例3：客户分类：利用庞大的客户信息将客户分类，区别精准服务.

 2.5 非监督学习算法2---异常检测算法、降维学习算法

只有输入特征x而没有标签y，算法自己寻找数据中的结构。

聚类学习算法：将相似的数据点归为一类。

异常检测：寻找异常点。

降维学习算法：使用更少的维度来压缩数据 。

 2. 6 Jupyter Notebooks

分为代码框和文本框

运行快捷键 Shif + Enter

3.1 线性回归模型part1

用线性回归预测房价：使用波特兰的房屋大小和价格数据集，横轴为房屋大小，纵轴为价格。每一个小十字都代表一个房子。如果有人问你一个房子能卖多少钱，这些数据可能会帮到你。

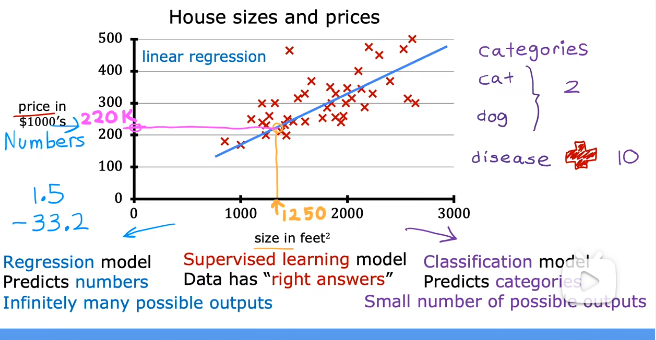
 先用线性拟合数据得出模型，再利用模型预测。

数据与图像一一对应。

 

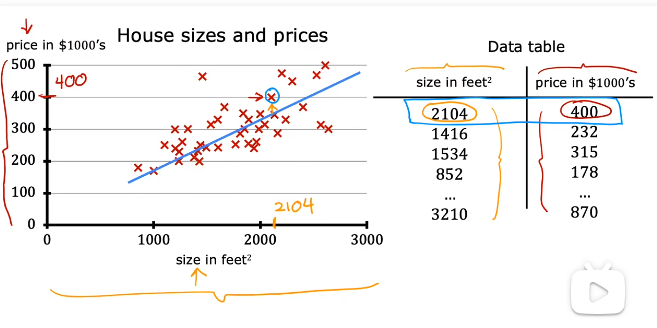
 机器学习术语：

x是输入特征，y是输出或者目标值

m代表训练集的样本个数

（x,y）代表一个样本

（x,y）代表第i个训练样本

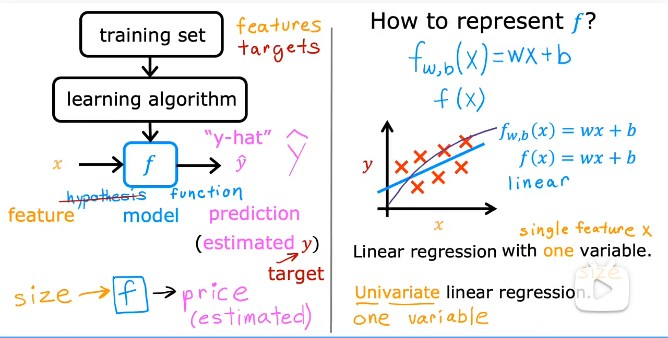
 训练集----> 学习算法----->模型------>预测

代表通过模型得到的预测值，y代表实际值，也是标签值。

f(x) = wx + b 单变量线性回归

3.3 损失函数

损失函数：表征模型拟合效果，利用损失函数优化模型。

线性模型中w，b是可以学习调节的参数。

 w和b的效果，w是斜率，b是截距，w控制倾斜角度，b上下移动

w=0 时，y恒等于b；

b=0时， y 恒过原点。

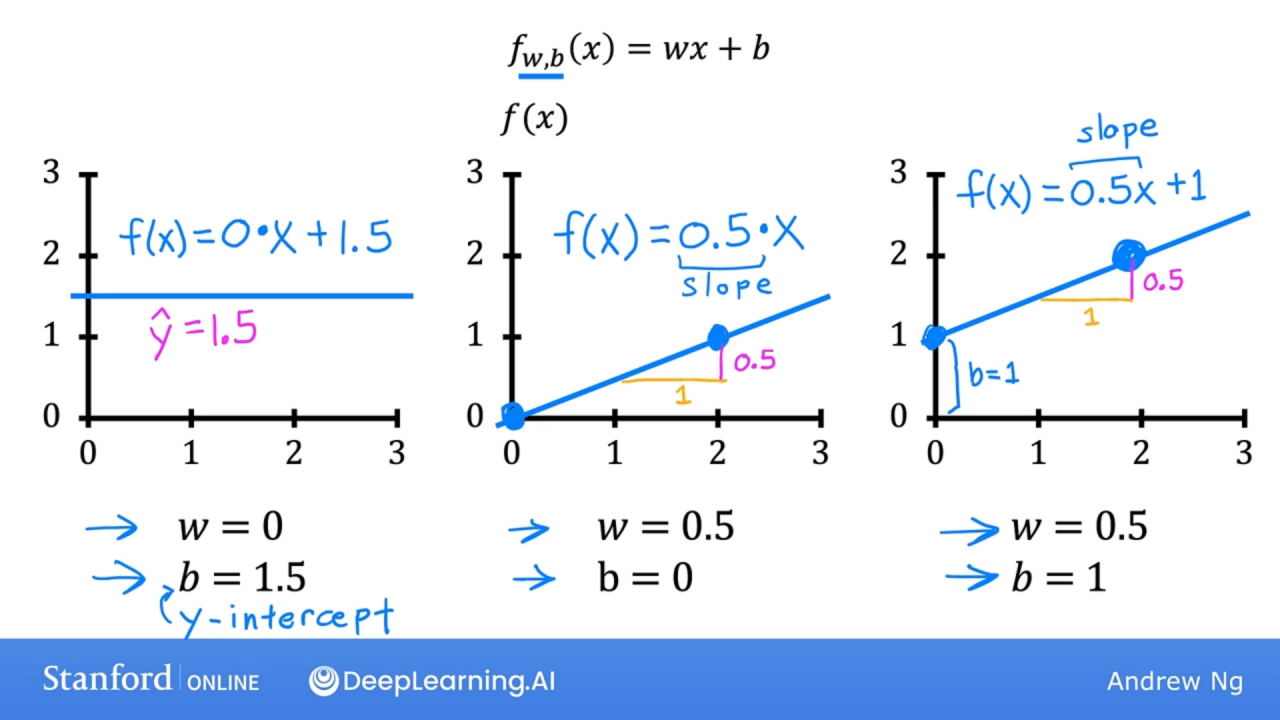
 理解损失函数的意义：即所有点的纵坐标到预测直线的距离的和的均值。

 平方误差损失函数。

3.4损失函数的直观理解

用损失函数为模型找到最佳参数。简化模型令b=0

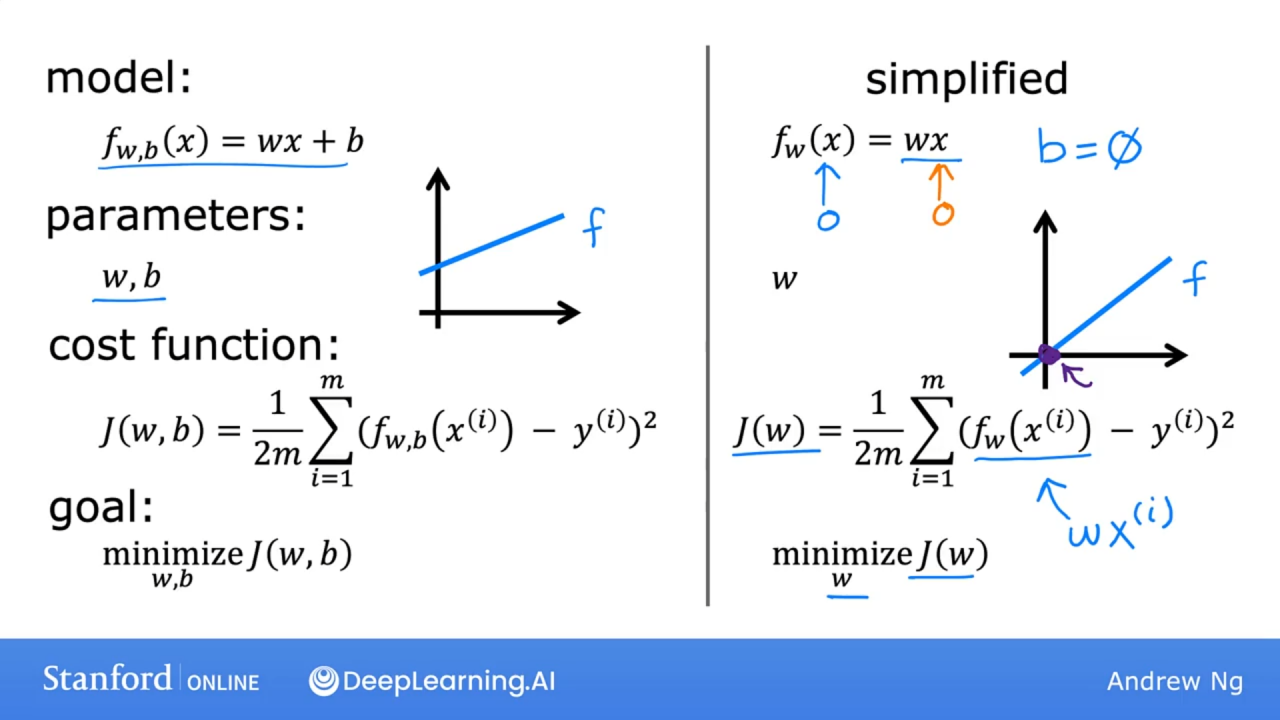
 w=1时，完全拟合，损失函数值为0

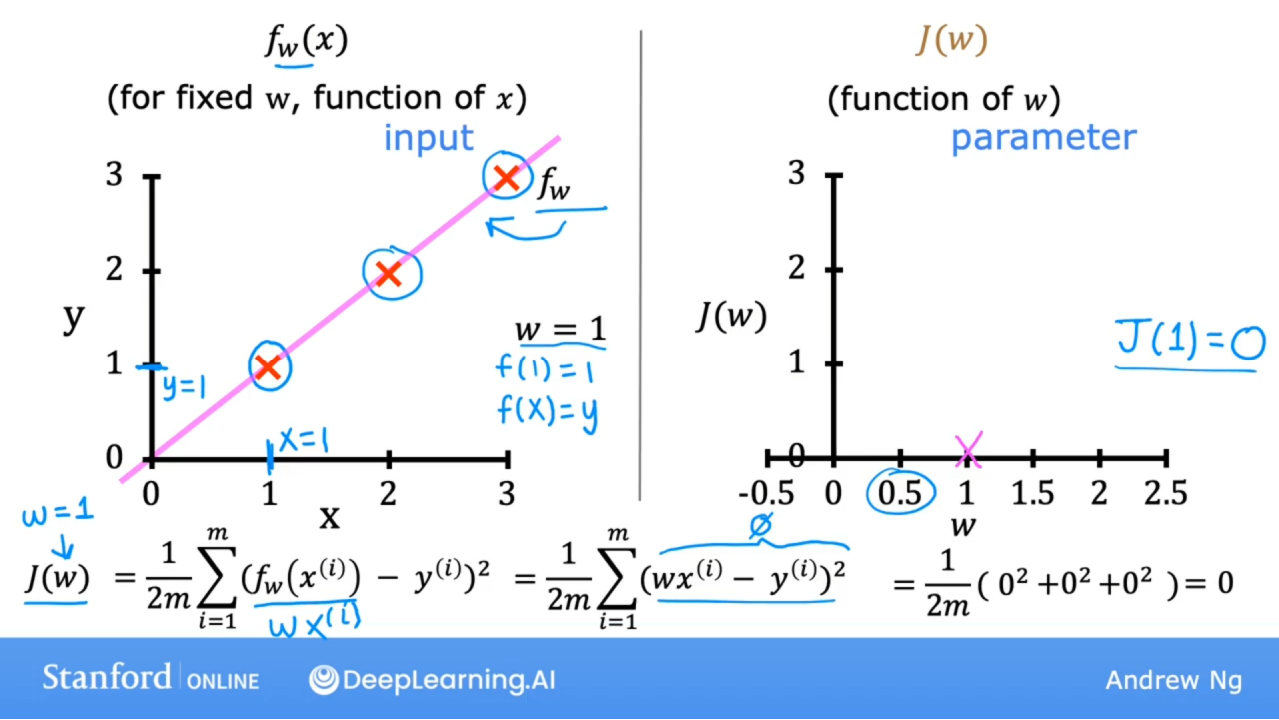
 w= 0.5时，损失函数值如下：

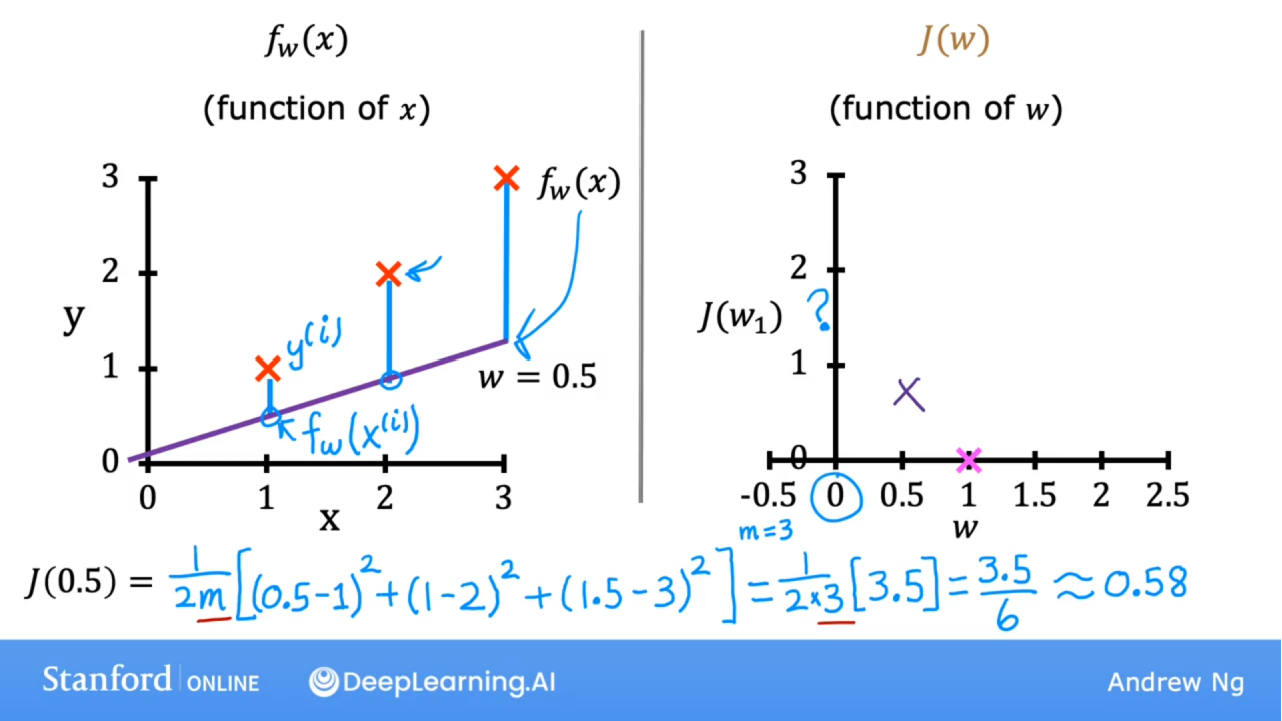
  w= 0时，损失函数值如下：其中w=0时，y=0，为x轴

=  

   = 

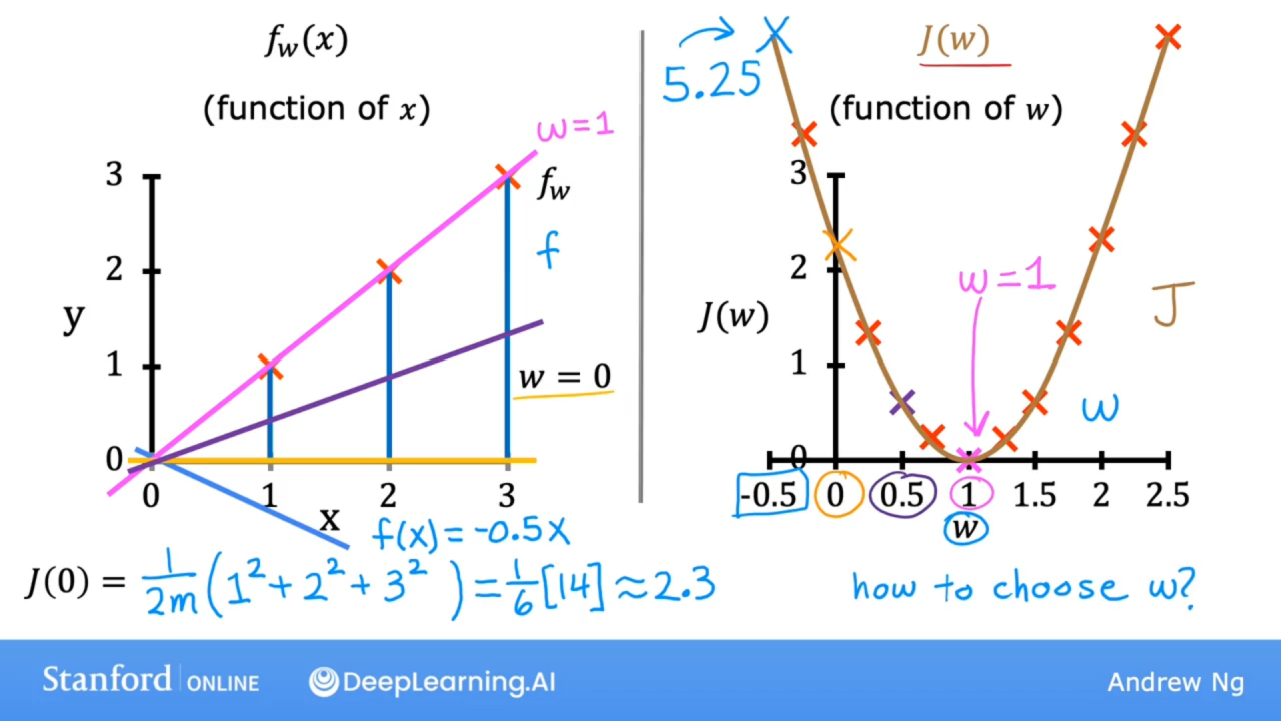
因为样本中x和y是定值，故损失函数是关于w的二次函数。

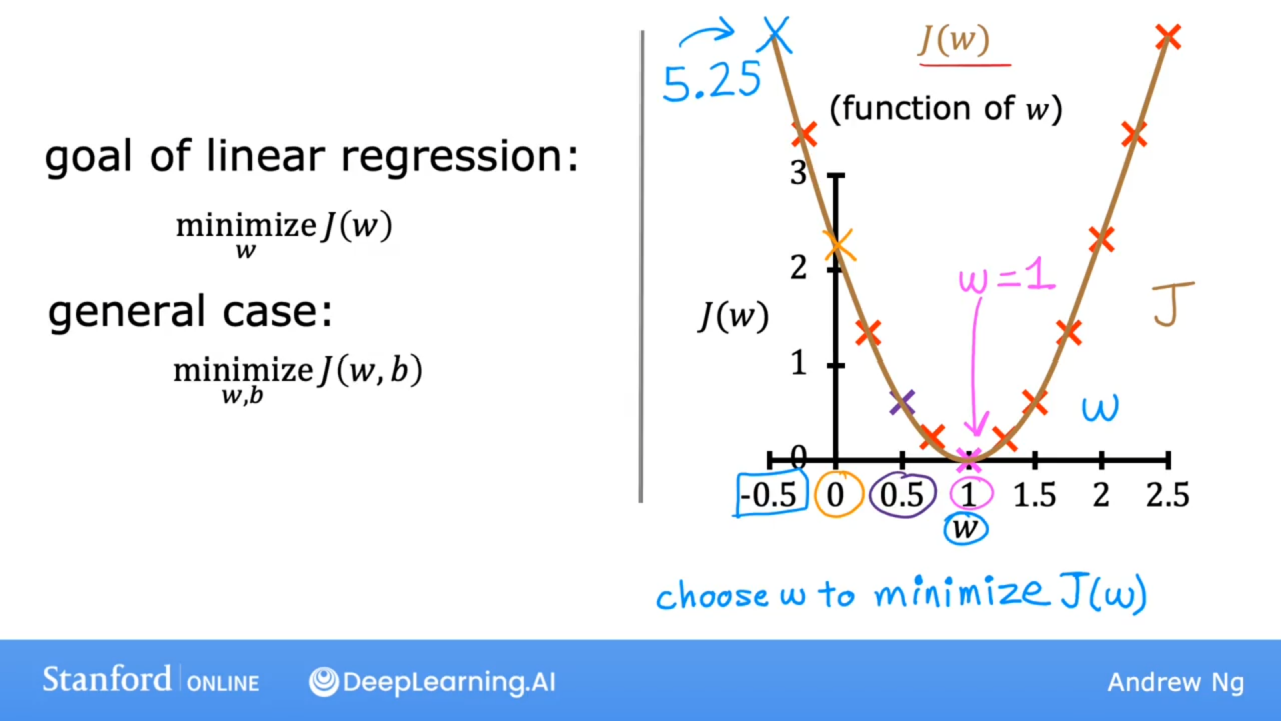
 现实中还有截距b

3.5 可视化损失函数

之前模型中令b=0，现在令b≠0

 下面的模型直线好像一直在低估房价，拟合不太好

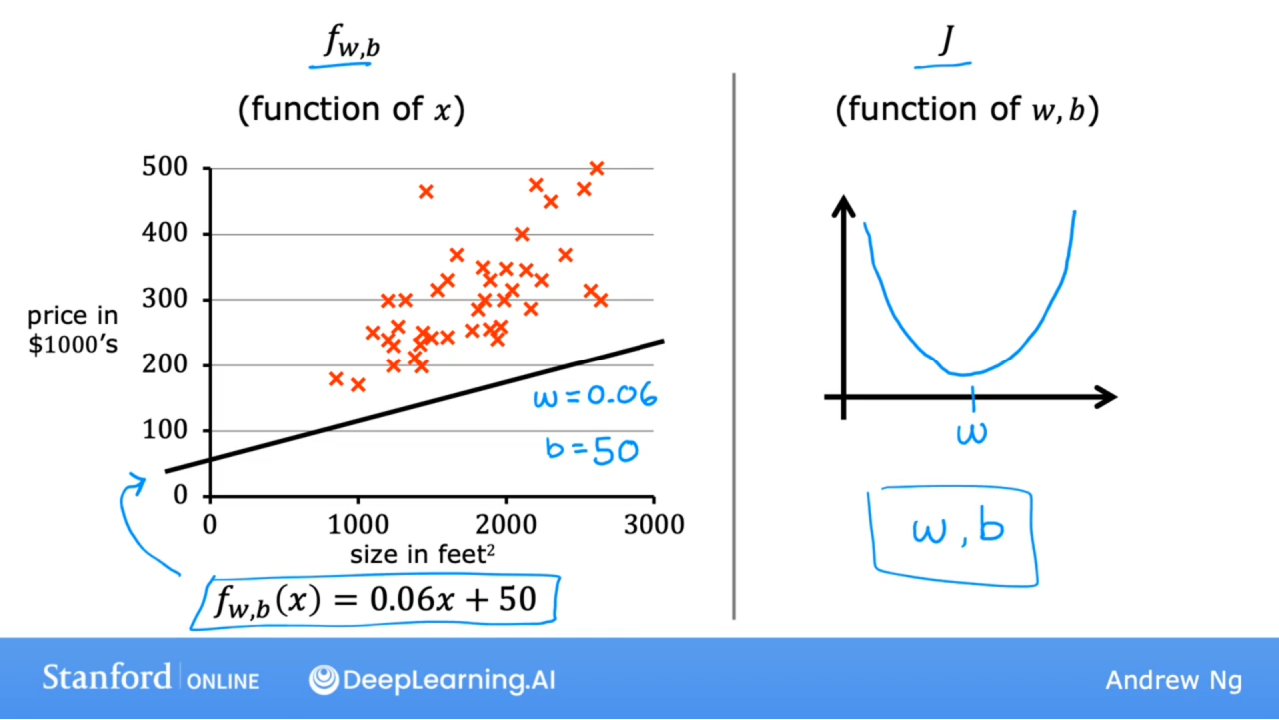
 w和b对J的影响

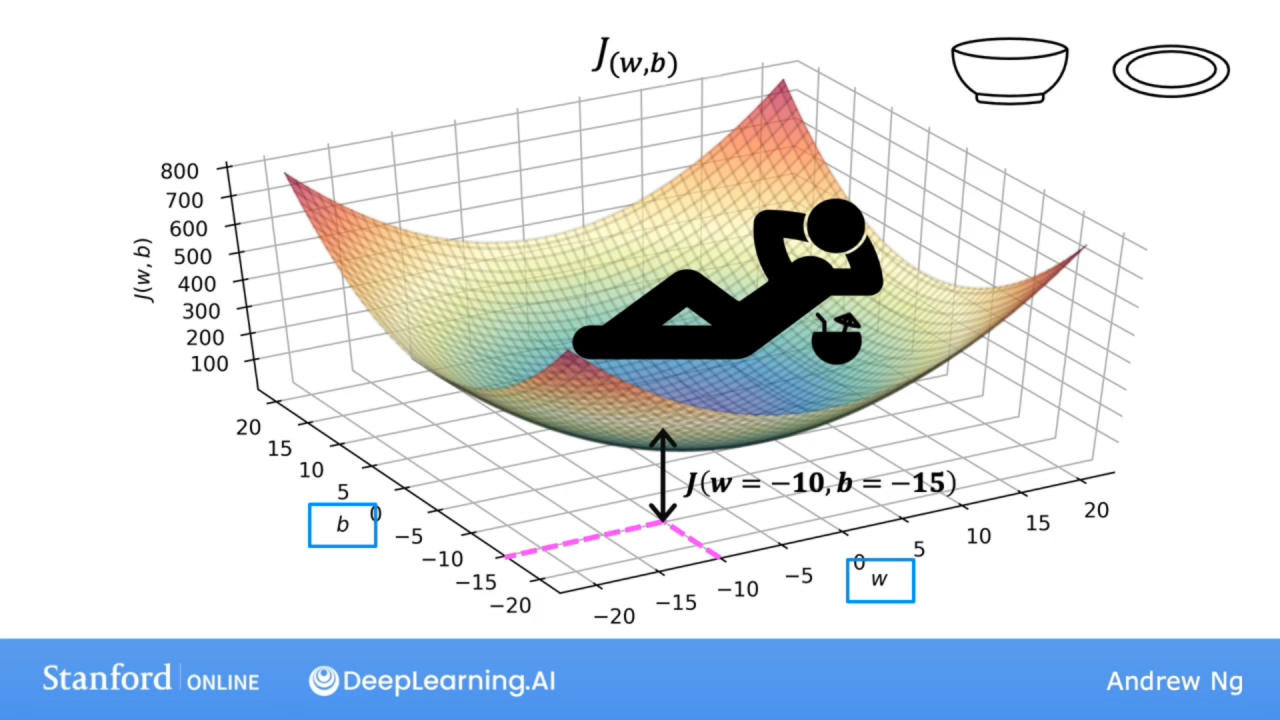
 固定w对b的截面就是二次函数曲线，梯度就是损失函数下降最快的方向，是一个向量。

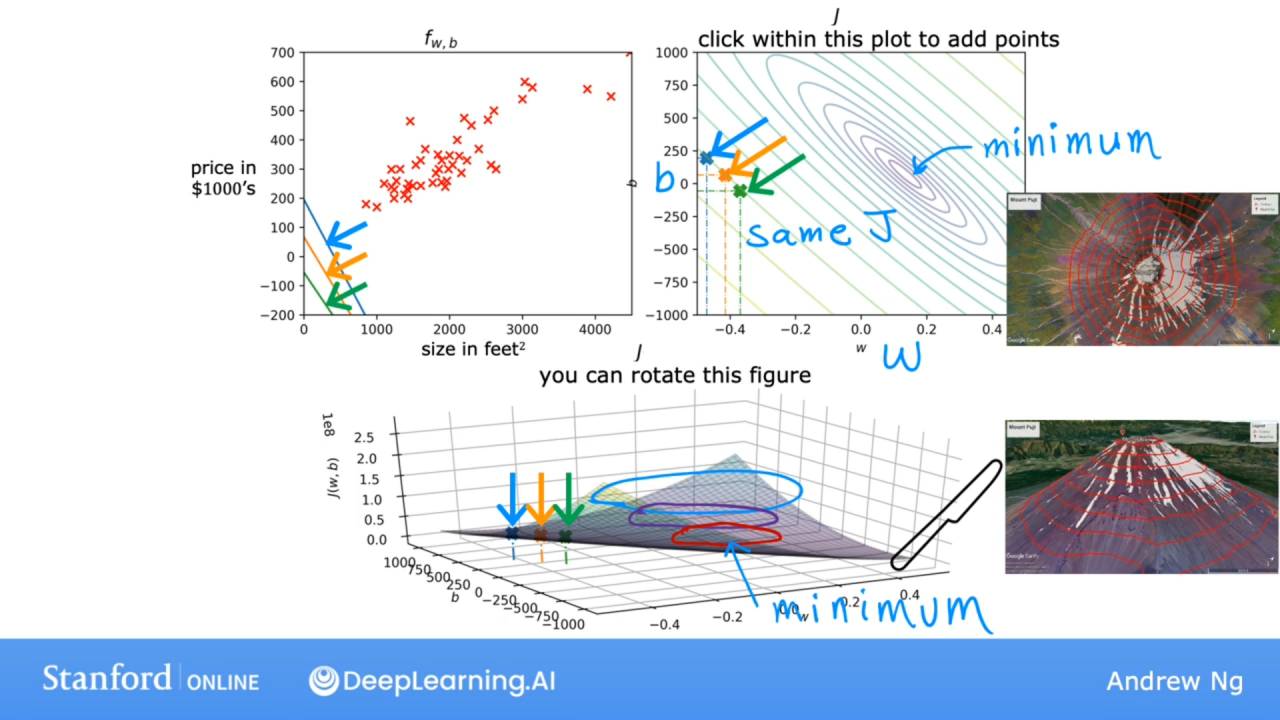
 用等高线反映曲线的取值，由于损失函数的特性，这是一个旋转抛物面，使得中心取值最小。

3.6可视化的例子