高精度数一般是指在计算中通常会遇到某个数的 位数可能达到几百或者更多，这类的数字统称为高精度数。首先我们通过下面这张图观察计算机中基本数据类型的信息，理解为什么需要使用高精度算法。

相比之下在基本数据类型中，对于整数来说，long long的取值范围大于int类型的取址范围，而long long类型能够存储的最大数值范围为 [-9223372036854775808,9223372036854775807]最大只能存储19位的数字且不能超过大于9223372036854775807，所以当我们要计算或操作的数据超过了该值，就无法使用基本的数据类型来实现对数值的使用。

例如：在十五届蓝桥杯算法竞赛中R格式这道题

该题以及明确说明了d字符串的长度范围是1~1024，想要对他进行相应的运算时就需要使用高精度算法。

接下来介绍关于正整数的高精度算法的原理和使用方法。

高精度加法

高精度加法的实现原理

讲解高精度算法首先我们从最基本，较为容易理解的高精度加法开始。
在进行加法运算时，我们通常都是使用竖式运算的方法来求解结果的，所以对于高精度数的加法也是如此，接下来我们从竖式运算的加法开始入手。

例如 计算数值A + B
假设A = 666，B = 88，那么使用竖式运算的实现方式如下：
首先按照A与B的每一位从低位到高位（从右往左）依次完成和运算得到结果如下：

按位相加以后当结果大于等于10（14）的时候需要保留当前数值的低位（4）然后向当前位的前面一个高位进行 + 1完成进位实现如下：

对于两个数的加法流程就是这样。 无论两个数多大通过这种方式都是能够得到结果的。

重温了一下加法竖式运算也许有的人看完之后自然会产生一点思路，对于高精度数的加法就是通过模拟常规的数学加法竖式运算，来实现求解高精度加法的结果。
在竖式运算中是从右往左依次计算每一位，进位的情况也是对当前位的前一位进行（右往左），由于高精度数的位数非常大，所以我们将它们使用字符串来存储，然后将他们从右往左从低位到高位逐个计算得出结果。为了方便将两个数的每一位逐个进行求和，我们使用vector对象来将两个数按照逆序进行存放。

还是以上面的A和B两个数值为例，建立两个vector对象分别来存储数值A和B的每一位，然后进行模拟求和运算。
通过对两个vector对象从左到右的遍历，模拟竖式加法中将两个数从地位到高位按位相加的运算，并完成相应的进位操作

对于这样两个数按照这个方式的表述可能容易引起误解，我们再举两个数值求和的实例。
例如 A = 567，B= 86则这样情况下用vector对象来存储A与B的情况应该是下面这样：

也就是说将数值的最低位（个位）放在[0]下标位置，然后按照按位数升上去依次存储。
完成每位的求和以后逆序输出result就得到了最终的结果。

高精度加法的代码实现

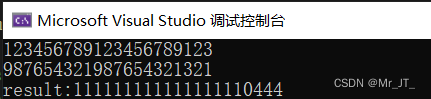
给定两个数为正整数时，求他们的和。

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

void getnum(vector<int>&temp, string num) // 将该数按照数组形式存储
{
	// 通过逆序进行存储，将低位的数值放在前面便于计算 
	for (int i = num.size() - 1;i >= 0;i--)
	{
		temp.push_back(num[i] - '0');
	}
}

vector<int> getres(vector<int>&num1, vector<int>&num2) // 将两个数模拟进行竖式相加，得到和运算后的结果
{
	vector<int>res;
	int t = 0; // 用来存储进位情况
	int end =  max(num1.size(),num2.size())
	for (int i = 0;i < end;i++)
	{
		int sum = t; // 将上一位相加结果是否进位作为初值
		if (i < num1.size()) sum += num1[i];
		if (i < num2.size()) sum += num2[i];
		res.push_back(sum % 10);
		t = sum / 10;
	}
	return res;
}
int main()
{
	string num_a;
	string num_b;
	// 获取两个操作数
	cin >> num_a;  
	cin >> num_b;
	// 用两个vector对象分别来存储数值中的每一位
	vector<int> temp_a;
	vector<int> temp_b;
	vector<int>res;
	getnum(temp_a, num_a);
	getnum(temp_b, num_b);
	res = getres(temp_a, temp_b);
	int n = res.size();
	cout << "result:";
	for (int i = n - 1;i >= 0;i--) // 逆序输出得到正确的和值
	{
		cout << res[i];
	}
	return 0;
}

程序测试结果如下：

高精度减法

高精度减法的实现原理

高精度减法与高精度加法类似也是通过模拟竖式运算来求得结果。与高精度加法不同的是，在减法中如果当前位数上的被减数小于减数时，被减数需要向它的前一位借一来完成运算。
对于两个正整数在进行减法的运算时，有可能会出现下面两种情况
①当被减数大于减数的时候：得到的结果是一个正数
②当被减数小于减数的时候：得到的结果是时一个负数，并且这个负数的绝对值等于减数与被减数的差。
因此在计算的时候无论两个数的大小关系，我们可以一直使用两个数中大的数减小的那个数来获取结果，如果小的数作为被减数输入的话就在结果前面加一个负号“-”。这样来就方便了运算。

高精度减法的代码实现

代码实现方式如下：

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

vector<int> getnum(string s) // 该函数实现将字符串每一位转为int并存放在vector对象中
{
	vector<int>temp;
	int n = s.size();
	// 逆序存放，低位在左边高位在右边
	for (int i = n - 1;i >= 0;i--)
	{
		temp.push_back(s[i]-'0');
	}
	return temp;
}

vector<int> sub(vector<int>&num_A, vector<int>&num_B) // 对A和B大小判断完成以后，A一定大于B
{
	vector<int>temp;
	int num_sub = 0; // 用来记录对应位的差值
	for (int i = 0; i < num_A.size();i++)
	{
		if (i < num_B.size()) // 防止越位访问
		{
			if (num_A[i] < num_B[i]) // 当对应位不够减时向前借一位
			{
				num_A[i] += 10;
				num_A[i + 1] -= 1;
				num_sub = num_A[i] - num_B[i];
			}
			else
			{
				num_sub = num_A[i] - num_B[i];
			}
		}
		else
		{
			num_sub = num_A[i];
		}
		temp.push_back(num_sub);
	}
	return temp;
}

// 实现高精度减法
int main()
{
	string A;
	string B;
	cin >> A;
	cin >> B;
	int len_A = A.size();
	int len_B = B.size();
	vector<int>num_A;
	vector<int>num_B;
	vector<int>res;
	bool isbig = 0;
	if (len_A < len_B || len_A == len_B && A < B) // 第一个数比第二个数小的时候进行交换，保证被减数大于减数
	{
		swap(A, B);
		isbig = 1; // 用来记录是否需要输出负号 "-"
	}
	num_A = getnum(A);
	num_B = getnum(B);
	res = sub(num_A, num_B);
	if (isbig)
	{
		cout << "-";
	}
	while (res.size() > 1 && res.back() == 0) res.pop_back();// 去除前导0
	reverse(res.begin(), res.end());
	for (int i = 0; i < res.size();i++)
	{
		cout << res[i];
	}
	return 0;
}

在网上也有很多不同的写法，有的写法看起来也比我的更简单，我的这种学法对于初学者来说可能能够更好的理解其中的实现方式。

---

总结

这篇文章目前记录的是高精度算法中两个高精度数的加法和减法运算的实现原理和实现方式。在算法竞赛中，高精度算法也是一个比较重点的类型，通过结合原理来学习代码的实现，这样能够加深对代码实现的印象。

---

临近期末啦，各科复习比较紧，高精度算法先写到这里，后续会更新高精度乘法与高精度除法，如果大家想继续学习的话，可以先点赞关注收藏喔！