🤵‍♂️ 个人主页：@rain雨雨编程

😄微信公众号：rain雨雨编程

✍🏻作者简介：持续分享机器学习，爬虫，数据分析
🐋 希望大家多多支持，我们一起进步！
如果文章对你有帮助的话，
欢迎评论 💬点赞👍🏻 收藏 📂加关注+

力扣	难度
112. 路径总和	🟢
113. 路径总和 II	🟠
654. 最大二叉树	🟠

---

目录

112. 路径总和

题目描述

思路步骤

代码实现

时间复杂度

空间复杂度

113. 路径总和 II

题目描述

思路步骤

代码实现

时间复杂度

空间复杂度

654. 最大二叉树

题目描述

思路步骤

代码实现

时间复杂度

空间复杂度

---

题目描述

给定一个二叉树的根节点 root 和一个表示目标和的整数 targetSum。要求判断该树中是否存在从根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum。如果存在，返回 true；否则，返回 false。

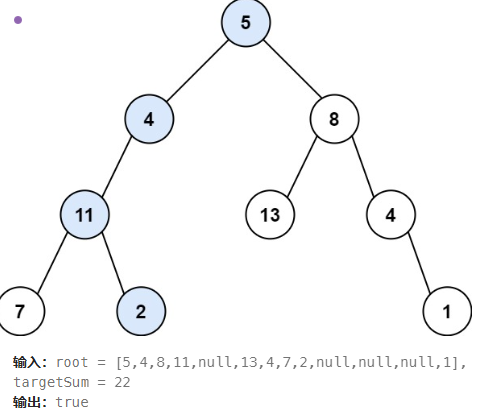
思路步骤

1. 定义基本情况：如果根节点为空，则不存在路径，返回 false。

2. 更新目标和：从目标和中减去当前节点的值。

3. 检查叶子节点：如果当前节点是叶子节点（没有左右子节点），则检查更新后的目标和是否为0，是则返回 true。

4. 递归左右子树：递归地检查左右子树，看是否存在满足条件的路径。

5. 合并结果：返回左右子树递归检查的结果，如果任一子树返回 true，则当前路径存在。

代码实现

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        // 基本情况：如果根节点为空，则不存在路径
        if(root == null) return false;
        
        // 更新目标和，减去当前节点的值
        targetSum -= root.val;
        
        // 检查当前节点是否为叶子节点，并且更新后的目标和是否为0
        if(root.left == null && root.right == null) {
            return targetSum == 0;
        }
        
        // 递归检查左右子树
        // 如果左子树或右子树存在满足条件的路径，则返回true
        return hasPathSum(root.left, targetSum) || hasPathSum(root.right, targetSum);
    }
}

时间复杂度

时间复杂度为O(n)，其中n为二叉树中的节点数。这是因为每个节点恰好被访问一次。

空间复杂度

空间复杂度为O(h)，其中h为二叉树的高度。这是因为递归过程中，最多会占用h层的栈空间，这是由于在最坏的情况下（树完全不平衡），递归的深度等于树的高度。

---

113. 路径总和 II

题目描述

给定一个二叉树的根节点 root 和一个整数目标和 targetSum，要求找出所有从根节点到叶子节点路径总和等于给定目标和的路径。叶子节点是指没有子节点的节点。

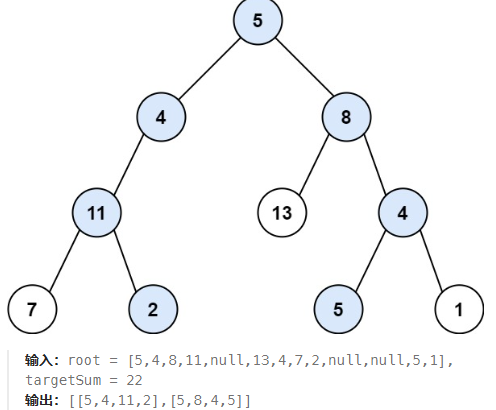
思路步骤

1. 定义基本情况：如果根节点为空，直接返回结果列表。

2. 使用路径记录：使用一个列表 path 来记录当前路径上的节点值。

3. 深度优先搜索（DFS）：从根节点开始，进行深度优先搜索。

4. 更新目标和：在遍历过程中，更新目标和 targetSum，减去当前节点的值。

5. 检查叶子节点：如果当前节点是叶子节点（没有左右子节点），并且更新后的目标和为0，则将当前路径添加到结果列表中。

6. 回溯：在递归左右子树后，从路径中移除当前节点，以探索其他路径。

7. 递归左右子树：对左右子树分别进行深度优先搜索，继续寻找符合条件的路径。

代码实现

class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        // 初始化结果列表和路径列表
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> path = new LinkedList<>();
        
        // 如果根节点为空，直接返回结果列表
        if(root == null) return res;
        
        // 从根节点开始深度优先搜索
        preorderdfs(root, targetSum, res, path);
        return res;
    }
    
    void preorderdfs(TreeNode root, int targetSum, List<List<Integer>> res, List<Integer> path) {
        // 将当前节点值添加到路径中
        path.add(root.val);
        targetSum -= root.val;
        
        // 如果当前节点是叶子节点，并且目标和为0，则将路径添加到结果列表中
        if(root.left == null && root.right == null) {
            if(targetSum == 0) {
                res.add(new ArrayList<>(path));
            }
        }
        
        // 如果左子树不为空，递归搜索左子树
        if(root.left != null) {
            preorderdfs(root.left, targetSum, res, path);
        }
        
        // 从路径中移除当前节点，以回溯探索其他路径
        path.remove(path.size() - 1);
        
        // 如果右子树不为空，递归搜索右子树
        if(root.right != null) {
            preorderdfs(root.right, targetSum, res, path);
        }
        
        // 从路径中移除当前节点，以完成当前节点的探索
        path.remove(path.size() - 1);
    }
}

时间复杂度

时间复杂度为O(N * M)，其中N是二叉树中的节点数，M是所有可能路径的数量。这是因为每个节点可能属于多条路径，我们需要检查每条可能的路径。

空间复杂度

空间复杂度为O(N)，这是因为在最坏的情况下，我们需要存储所有节点的路径，这将需要N个空间来存储路径上的节点值。另外，递归栈的深度最多为树的高度，即O(logN)，但在最坏情况下，树可能是一条链，因此递归栈的深度可以是N。

---

654. 最大二叉树

题目描述

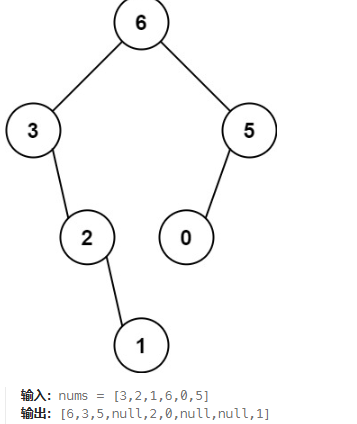
给定一个不重复的整数数组 nums，要求使用这些整数构建一个最大二叉树。构建规则如下：

1. 创建一个根节点，其值为 nums 中的最大值。

2. 递归地在最大值左边的子数组前缀上构建左子树。

3. 递归地在最大值右边的子数组后缀上构建右子树。

4. 返回由 nums 构建的最大二叉树。

思路步骤

1. 定义基本情况：如果子数组长度小于1，返回 null。

2. 找到最大值：在当前子数组中找到最大值及其索引。

3. 创建根节点：以最大值为根节点创建一个新的二叉树节点。

4. 递归构建左子树：在最大值左边的子数组上递归构建左子树。

5. 递归构建右子树：在最大值右边的子数组上递归构建右子树。

6. 合并结果：将左子树和右子树分别赋值给根节点的左右子节点，并返回根节点。

代码实现

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        // 调用递归函数构建最大二叉树
        return constructMaximumBinaryTree1(nums, 0, nums.length);
    }
    
    TreeNode constructMaximumBinaryTree1(int[] nums, int leftIndex, int rightIndex){
        // 基本情况：如果子数组长度小于1，返回null
        if (rightIndex - leftIndex < 1) return null;
        
        // 基本情况：如果子数组长度为1，返回一个只含该节点的树
        if (rightIndex - leftIndex == 1) return new TreeNode(nums[leftIndex]);
        
        // 寻找最大值及其索引
        int maxIndex = leftIndex;
        int maxVal = nums[leftIndex];
        for (int i = leftIndex + 1; i < rightIndex; i++) {
            if (maxVal < nums[i]) {
                maxVal = nums[i];
                maxIndex = i;
            }
        }
        
        // 创建根节点
        TreeNode root = new TreeNode(maxVal);
        
        // 递归构建左子树
        root.left = constructMaximumBinaryTree1(nums, leftIndex, maxIndex);
        
        // 递归构建右子树
        root.right = constructMaximumBinaryTree1(nums, maxIndex + 1, rightIndex);
        
        // 返回构建的最大二叉树
        return root;
    }
}

时间复杂度

时间复杂度为O(n^2)，其中n为数组 nums 的长度。这是因为在每次递归中，我们需要遍历整个数组来找到最大值，这个操作需要O(n)时间，而总共有O(n)次递归。

空间复杂度

空间复杂度为O(n)，这是因为递归栈的深度最多为n，即数组的长度。在最坏的情况下，树可能是一条链，因此递归栈的深度可以达到n。

文章持续跟新，可以微信搜一搜公众号  [ rain雨雨编程 ]，第一时间阅读，涉及数据分析，机器学习，Java编程，爬虫，实战项目等。